2. Direction-distance
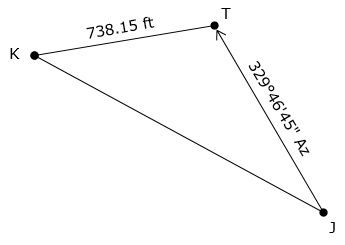
Figure xx-2 is a diagram of a base line and an intersection point.
|
|
|
Figure E-2 |
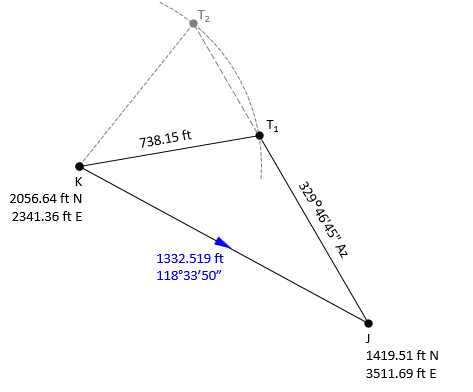
Coordinates of the base line end points are:
| Point | North (ft) | East (ft) |
| J | 1419.51 | 3511.69 |
| K | 2056.64 | 2341.36 |
The azimuth from point J to point T is 329°46'45"; the distance from point K to point T is 738.15 ft.
What are the coordinates of point T?
Step (1) Inverse the base line from point K to point J
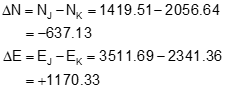
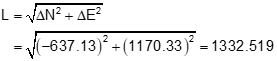

![]()
a. Triangle-based method
To get point T's coordinates, we'll perform a forward computation from K.
Step (2) Compute the angle at J
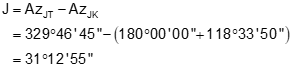
Step (3) Use Law of Sines to compute angle at T
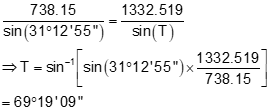
Remember that we have to check the angle returned by the Law of Sines because it will always be <90°.
From the diagram, T is greater than 90° so it must be subtracted from 180°
![]()
Step (4) Compute angle at K from the Angle Condition
![]()
Step (5) Compute azimuth from point K to point T
![]()
Step (6) Forward compute from point K
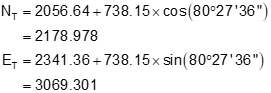
The math check is to compute the coordinates from point J
Step (1) Compute distance from point J using Law of Sines
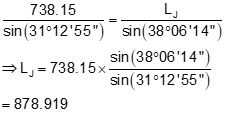
Step (2) Forward compute from point J

b. Arc-based method
Because the direction can intersect the arc at two points, we'll extend the diagram a bit to visualize the possibilities, Figure XX-XX.
|
|
|
Figure E-3 |
Step (2) Set up and solve Equations D-12 through D-15.
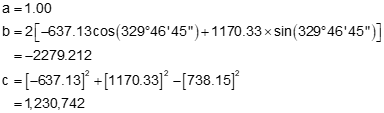
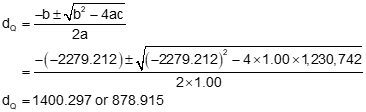
Step (3) Pick the correct distance and compute the coordinates
From Figure E-3, the correct distance dQ is the shorter one: 878.915,. Using that distance, perform a forward computation
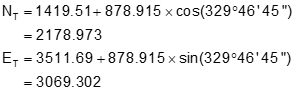
The coordinates of point T are the same as those from the triangle-based method.