4. Network adjustment example 2
a. Data
The diagram below shows a link circuit running from BM Lima to BM Hotel.
are instrument locations.
TP# is a temporary turning point.
Green numbers are elevations determined in the field.
Blue numbers are BS and FS distances in paces measured by the rod person.
The rod person's pace count is 41.5 paces per 100.0 ft.
Known elevations are BM Lima = 926.49' and BM Hotel = 953.41'
Because the network ended on BM Hotel, we use its measured and known elevations to determine the misclosure, M:
M=953.49' - 953.41'= +0.08'
b. Equal distribution
A total of 7 elevations were established. From Equation E-1:
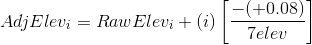
Applying the equation to each non-turning point:
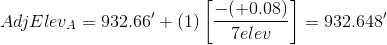
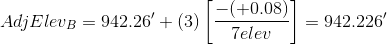
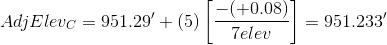
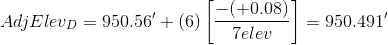
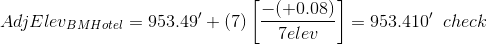
We don't need to adjust the turning point elevations, we just need to keep track of the sequential number of the elevation that is being adjusted. As a math check, we always compute the adjusted elevation of the closing point.
c. Proportional distribution
The total sight length of the network is:
(53p+54p+39p+39p+62p+61p+46p+47p+29p+28p+66p+68p+31p+32p) = 655p
We could use the rod person's pace count to convert 655p to feet, but we don't need to. Why not? Because the paces will cancel in the elevation adjustment equation.
From Equation E-2:
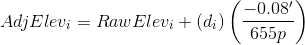
To adjust the elevation of A:
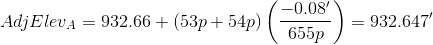
Cumulative and total distance units cancel.
Before continuing with the rest, let's compute the cumulative distance to each point so our adjustment equations don't become too cumbersome.
A: 54p+54p = 107p
TP1: 107p+39p+39p = 185p
B: 185p+62p+61p = 308p
TP2: 308p+46p+47p = 401p
C: 401p+29p+28p = 458p
D: 458p+66p+68p = 592p
BM Hotel: 592p+31p+32p = 655p
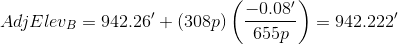
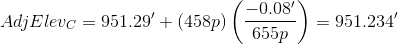
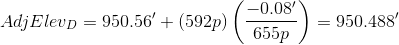
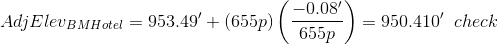
Although we didn't adjust turning points elevations, we included the distances through them to points that were adjusted.
