2. Natural
a. Climate
(1) Description
Weather can have various detrimental effects on leveling accuracy:
- Heat waves are atmospheric anomalies that can randomly bend the LoS or make the rod difficult to read.
- Wind gusts will cause the compensator to bounce as well as make it a challenge to hold an extended level rod vertical.
- A large temperature difference between equipment storage and use requires acclimation time or tripod leg locks may loosen and slip.
- Cold uncomfortable temperatures can result in haphazard work.
(2) Behavior
Cumulative effect is random.
(3) Compensation
In as much as possible select times and locations minimizing climate impacts. Allow equipment temperature acclimation. Dress for conditions.
b. Curvature
(1) Description
Recall that a level line is curved and the LoS is horizontal. Both coincide at the instrument but separate as the distance from the instrument increases.
(2) Behavior
Figure D-11 shows that curvature causes the rod reading to be too high.
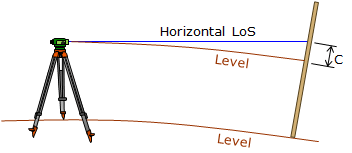 |
| Figure D-11 Curvature Error |
The effect of curvature is systematic; it is a function of distance, Equation D-1.
| c = -0.667M2 = -0.0239F2 | Equation D-1 | |
| c: reading correction, ft M: distance to rod, miles F: distance to rod, 1000s of ft |
||
Note: F in 1000s of feet means, for example, that at 100 ft, F = 100/1000 = 0.1
(3) Compensation
(a) Mathematical - Curvature can be accounted for by computing and applying the correction, Equation D-1, to the rod reading.
(b) Procedural - Because curvature is a function of distance, balancing BS and FS distances, Figure D-12, allow it to cancel: CBS (added) is the same as CFS (subtracted).
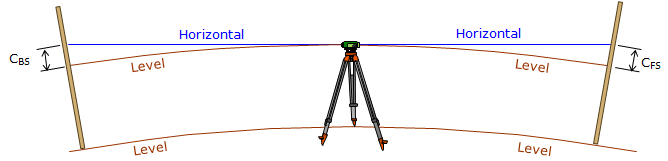 |
| Figure D-12 Curvature Compensation |
c. Refraction
(1) Description
Even if there are no atmospheric anomalies, the fact that the LoS has to pass through atmosphere causes it to bend, introducing a reading error.
(2) Behavior
Refraction causes the LoS to be bent downward, Figure D-13, resulting in a rod reading that is too low.
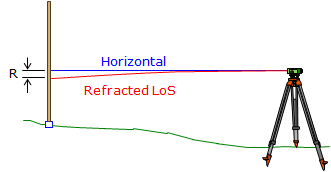 |
| Figure D-13 Refraction Error |
The effect of refraction is systematic and is a function of distance, Equation D-2.
| R = +0.093M2 = +0.0033F2 | Equation D-2 |
| R: reading correction, ft M: distance to rod, miles F: distance to rod, 1000s of ft |
|
(3) Compensation
(a) Mathematical - Refraction can be accounted for by computing and applying the correction, Equation D-2, to the rod reading.
(b) Procedural - Being a function of distance, balancing BS and FS distances allows refraction to cancel, Figure D-14: RBS (added) is the same as RFS (subtracted).
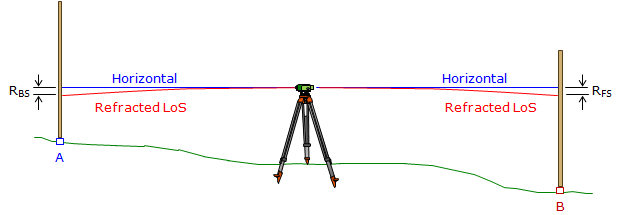 |
| Figure D-14 Refraction Compensation |