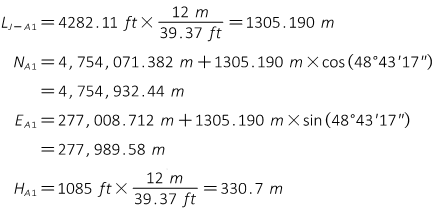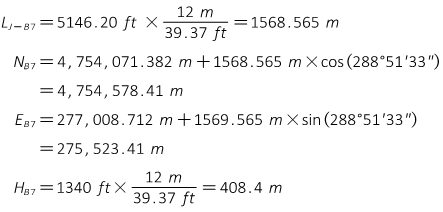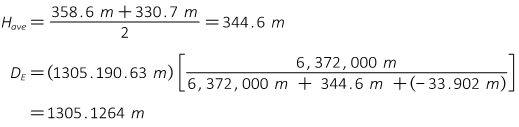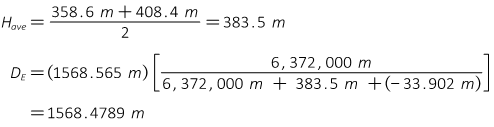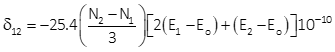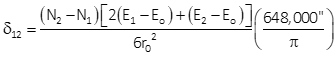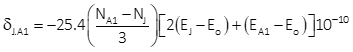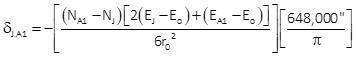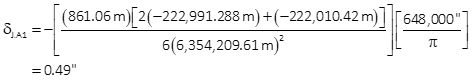L. Reduction Example: UTM
1. Preliminary Calculations
a. Survey Data
This chapter covers measurements reduction for a UTM cylindric zone.,
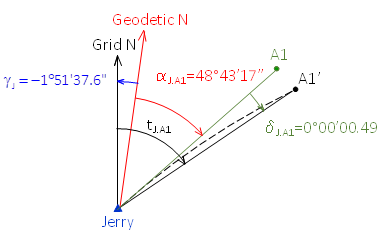
The survey data and UTM grid information for point Jerry are summarized in Figure L-1 and Table L-1.
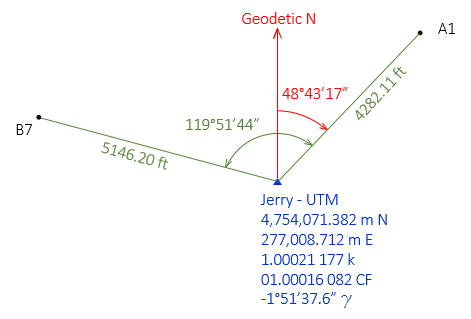 |
| Figure L-1 Survey Data |
| Table L-1 Orthometric Heights |
|
| Point |
H, ft |
| Jerry | 1177 |
| A1 |
1805 |
| B7 |
1340 |
b. Lengths, Coordinates and Orthometric Heights
Convert lengths and orthometric heights to meters; compute approximate UTM coordinates of A1 and B7.
Point A1
Point B7
Point Jerry
From its datasheet: orthometric height is 358.6 m.
2. Ground Distance to Grid
a. Ground to Ellipsoid
 |
| Figure L-2 Ground to Geodetic |
We computed geodetic distances in Chapter K - those can be converted to meters to use here.
However, we'll do the computations from scratch using Equation H-2 to.
Jerry's -33.902 meter geoid height will be used as a project average.
Equation H-2
(1) Geodetic distance Jerry-A1
(2) Geodetic distance Jerry-B7
b. Ellipsoid to Grid
 |
| Figure L-3 Geodetic to Grid |
We'll use and compare the same reductions for UTM as we did for SPC. Table L-2 shows the grid scale at each point and how they were obtained.
| Table L-2 Grid Scales |
||
| Point |
Scale |
Source |
| A1 | 1.00020 6404 | software |
| Jerry-A1 midpoint | 1.00020 9086 | Equation H-4 |
| Jerry | 1.00021 177 | datasheet |
| Jerry-B7 midpoint | 1.00021 5856 | Equation H-4 |
| B7 | 1.00020 8953 | software |
Jerry's CF from the datasheet is 1.00016 082.
Because the process is similar to SPC grid reduction, computations are not shown but results are summarized in Tables L-3 and L-4.
DE x k k
Grid Dist, m
Diff, m
Wtd Ave k 1.00020 9086 1305.3993
- -
Average k 1.00020 9087
1305.3993
0.0000
Jerry's k 1.00021 177
1305.4028
+0.0035
Combined Factor DH x CF 1.00016 082
1305.4000
+0.0007
Unlike SPC reduction, using Jerry's scale as a project average resulted in the largest differences. Average line scale worked well. Jerry's CF reduction had small (inconsequential?) differences. Using CF reduction could be sufficient if the elevations of points A1 and B7 represent the range across the project.
DE x k k
Grid Dist, m
Diff, m
Wtd Ave k 1.00021 4025
1568.8175
- -
Average k 1.00021 0362
1568.8175
0.0000
Jerry's k 1.00021 177
1568.8111
-0.0064
Combined Factor DH x CF 1.00016 082
1568.8173
-0.0002
3. Grid Direction
To convert the geodetic azimuth of line Jerry-A1 to grid, in addition to convergence we need to know:
- where the two meridians are with respect to each other, and
- if the arc-to-chord correction is significant
a. Meridians
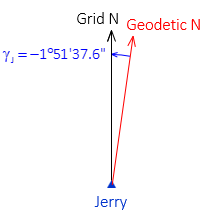
Convergence is the angle from Geodetic N to Grid N. Jerry's UTM convergence is -1°51'37.6". Because it is negative, Geodetic N is east of Grid N, Figure L-4.
Figure L-4
Geodetic and Grid North
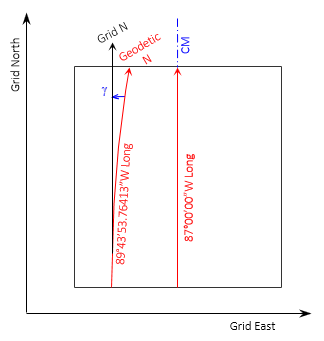
We can also determine the relationships by comparing longitudes. Jerry's coordinates are in UTM Zone 16 whose CM is at 87° W longitude. Jerry is west of the CM at 89°43'53.76403" W longitude, Figure L-5, placing Geodetic N east of Grid N
Figure L-5
Longitudes
b. Arc-to-Chord
The arc-to-chord correction for line Jerry-A1 can be computed using either Equation H-11 or H-12. We'll use both to see if there's a difference.
Equation H-11 Equation H-12
Both equations require Eo which is a defining zone parameter: it is the east coordinate of the CM (false easting). Eo is 500,000.00 m for all UTM zones.
(1) Using Equation H-11
Equation H-11 is set up for metric coordinates so we don't need to convert any points. Set up in terms of point identifiers:
Coordinate differences:
Substituting into the correction equation:
(2) Using Equation H-12
Equation H-12 in terms of point identifiers is:
This equation requires ro which is constant for for a zone but not given as a defining parameter. NCAT does not provide this information but the NAD 83 Coordinate Conversion workbook does.
For UTM Zone 16, ro = 6,354,209.61 m
Substituting coordinate differences into the correction equation:
(3) Application
As expected (with fingers crossed) both equations yield the same result.
Is the arc-to-chord correction significant? That's up to the surveyor and the type of project. Even though it's less than a second, we'll apply it as it may affect rounding.
To compute the Grid Azimuth from Geodetic, convergence, and arc-to-chord correction, use Equation H-7.
Equation H-7
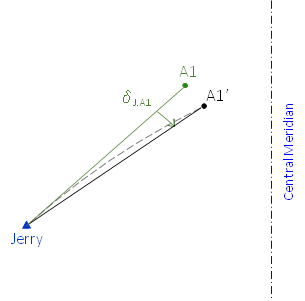
Another way to determine the correction's behavior is by examining the line's position relative to the CM. In a transverse cylindric projection the projected line is concave toward the CM. Line Jerry-A1 is west of the CM so it is concave to the east, Figure L-6.
Figure K-6
Line Jerry-A1 Concavity
Putting the pieces together, Figure K-7, it's apparent that the correction's value must be added in Equation H-7.
Figure K-7
Grid Azimuth
Using Jerry's convergence and the negative arc-to-chord correction, the Grid Az of Jerry-A1 is:
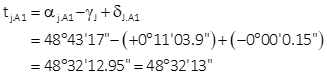
4. Ground to Grid Angle
To convert angle B7-Jerry-A1 to grid, we need the arc-to-chord correction for lines Jerry-A1 and Jerry-B7. We have the former, now must compute the latter. Although line Jerry-B7 is longer it is oriented more east-west than Jerry-A1 so the magnitude of its arc-to-chord correction should be smaller..
Since we've already shown that Equations H-11 and H-12 give that same results, we'll use the latter to compute the correction.
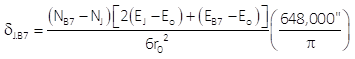
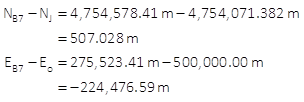
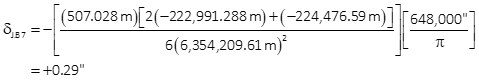
As expected, because of the line orientation, its arc-to-chord correction is smaller.
Figure K-8 is a sketch of the angle with all parts in place.
 |
| Figure K-8 Angle Correction |
The grid angle B7'-Jerry-A1', βG , is:
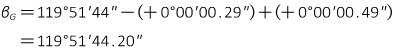
The total effect of the backsight and foresight arc-to-chord corrections amounts to only 00.20" which may be small enough to disregard.
5. Summary
In this example, we looked at a few different grid reduction methods. Depending on the accuracy needs of the survey, simple methods may be fine to use instead of more complicated (and time consuming) ones. The decision should be based on examination of worse-case scenarios.
If the two lines of the example survey represent the extreme situations, we determined that
- distance reduction - Jerry's grid scale could be used for the entire project but each line should use its own average elevation
- arc-to-chord correction - was probably not significant enough to affect directions or angles.