2. Drawbacks?

Geographic coordinates are simple, but they do have some disadvantages.

a. Spherical trigonometry

(1) Distances

Distances between points are arcs, Figure B-2. Their lengths are angular and must be determined using spherical trigonometry.

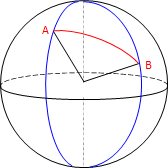Figure B-2 Arc Distance

Survey distances are measured in linear units so another computational layer is added to make them work with geographic coordinates

(2) Angle Conditions

Multi-sided figures have curved sides and the Σ (interior angles)=(n-2)x180° angle condition does not apply, For example, the interior angle sum of triangle CDE in Figure B-3 can exceed 180°00'00".

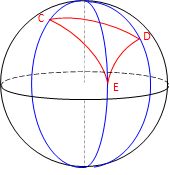Figure B-3 Spherical Triangle

The amount by which the angle condition is exceeded is called spherical excess and accumulates at approximately 0°00'01" per 70 square miles of enclosed area.

b. Meridian convergence

(1) Directions

Meridians are parallel at the equator and converge to a point at the poles, Figure B-4 

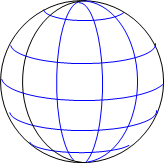Figure B-4 Convergence

• Except for due east-west or north-south lines, forward and back directions are not exactly 180° degrees apart.
• Because they are perpendicular to meridians, east-west lines are curved not straight.
• A uniform angular difference between meridians is not uniform length. In Figure B-5, The longitude difference from G to F is the same as from K to J, but the arc distance GF is longer than KJ. This is true for any angle difference that is not along a meridian.

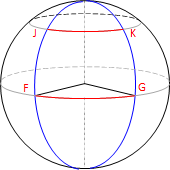Figure B-5 Length Variation

c. The earth isn't round

Geographic coordinates are based on a sphere. Unfortunately the Earth is not spherical. A different geometric model is needed which complicates things. We still use latitude and longitude positions, but their geodetic counterparts, not geographic. This may seem a trifling difference, but it isn't, and will be covered in a subsequent chapter.