6. Examples
Example (1)
Photography was taken with a 6.00 inch focal length camera flown at an height of 3500 ft above datum. Appearing on the photo are points J and K, whose elevations are 812.1 ft and 887.9 ft respectively. What are the photo scales at those points?
Solution

Example (2)
The elevation of points S and T is 703.6 ft and horizontal distance between them is 455.0 ft. The photo distance between the same two points is 32.1 mm. If the focal length of the camera used is 153.67 mm what was the flying height of the camera?
Solution
Set up Equation C-2
![]()
Set up Equation C-1
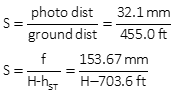
Set them equal to each other and solve the flying height
Example (3)
Figure C-12 is a portion of a Wis Dept of Trans aerial photo of Madison, WI. The camera's focal length was 152.265 mm (calibrated), flying height 3790 ft, and photo size 9 in by 9 in..
 |
| Figure C-12 Madison Aerial Photo |
The yellow lines connect opposite side fiducials, their intersection is the principal point. The large four-wing structure is the state capitol building and almost coincides with the principal point.
At the lower right of the image, a building edge is circled in red, Figure C-13 shows a magnified view.
 |
| Figure C-13 Building Detail |
Measured distances from the principal point to the bottom and top of the building edge are 55.03 mm and 56.80 mm. The area around the building is relatively flat with an elevation of 920 ft.
What is the building height?
Solution:
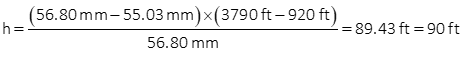
Example (4)
Two control points were targeted so they would appear in the aerial photography. Their Dane County Coordinates and elevations are:
| Point | North (ft) | East (ft) | Elev (ft) |
| T101 | 481,453.94 | 818,331.87 | 852.80 |
| T102 | 481,982.17 | 820,906.02 | 917.99 |
Their photo coordinates were measured
| Point | x (mm) | y (mm) |
| T101 | -57.58 | 49.02 |
| T102 | 64.37 | -15.18 |
The calibrated focal length of the camera was 152.265 mm.
What was the flying height?
There are two ways to compute flying height with the provided information: (1) Scale and (2) Ground Coordinates.
Scale Method
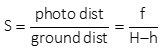
Compute photo (d) and ground (D) distances from the coordinates. Use the average elevation for the line between control points.
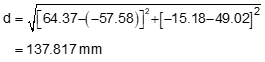
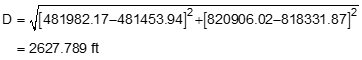
![]()
Re-sort scale equation to solve for H:
![]()
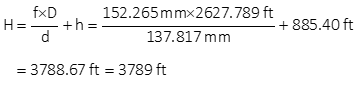
Flying height, H, is 3790 ft
Using Ground Coordinates.
Ground coordinates are related to photo coordinates by the scale. The ground coordinates we have for the control points are not based on the photo so we can't just solve equations C-3 and C-4 backwards to get H. The ground distance between the control points is the same wether we use the Dane County or photo Ground coordinates.
The inverse distance equation in terms of photo Ground coordinates is:
![]()
Substitute in Equations C-3 and C-4 and sort terms:
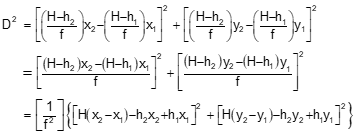
Since we know D=2627.789 ft by inversing Dane Co coords, the only unknown is H.
Input the numbers we know:

We're left with a second degree polynomial which requiring a quadratic solution:

Of the two possible answers, 3790 is the one that makes sense.
Flying height, H, is 3790 ft
Which is the right answer?
In this case, both methods gave the same result. Technically, the Ground Coordinate method is better because the Scale method uses an average elevation. If there were a substantial elevation difference between endpoints, using an average might introduce an error.
