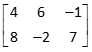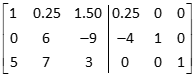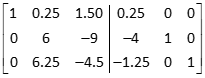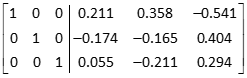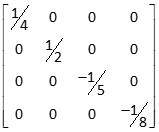4. Matrix Operations
a. Transposition
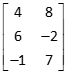
Transposing a matrix means to flip its rows and columns.
|
|
transposed is |
|
A transposed matrix is identified with a T superscript: m[B]n transposed is n[BT]m.
b. Determinant
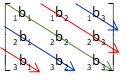
The determinant of a matrix is the difference between the sums of the diagonal multiplications in one direction and sums of the diagonal multiplications in the other direction. It is a number and generally denoted as ||B||.
|
It can be graphically depicted as: |
|
|
|
|
|
A 0 determinant means the matrix is singular.
c. Addition and Subtraction
Two matricies with the same dimensions can be added. Corresponding elements in each matrix are added, or subtracted, to create the corresponding element in the result matrix.
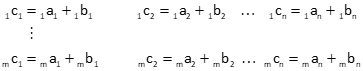
The final matrix has the same dimensions as both addend matrices: m[A]n + m[B]n = m[C]n
d. Scalar Multiplication
A scalar is a constant. Each matrix element is multiplied by the scalar: k x m[A]n = m[kA]n
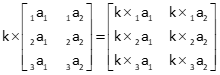
e. Matrix Multiplication
The number of columns in the first matrix must match the number of rows in the second. The product matrix will have the same number of rows as the first matrix and the same number of columns as the second.
m[A]n x n[B]p = m[C]p
The product element is the sum of each row element in the first matrix multiplied by the corresponding column element in the second matrix.
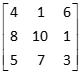
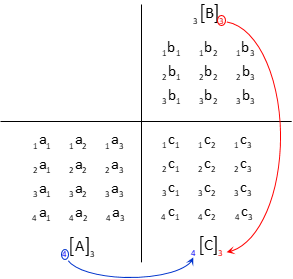
For example, multiplying 4[A]3 by 3[B]3 to obtain 4[C]3, elements of the [C] matrix are:
Column 1
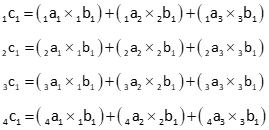
Column 2
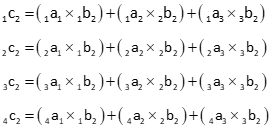
Column 3
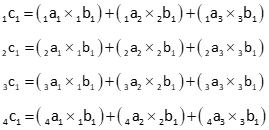
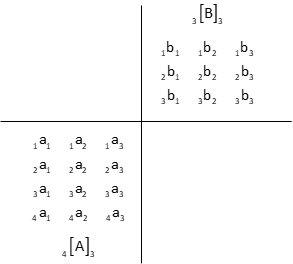
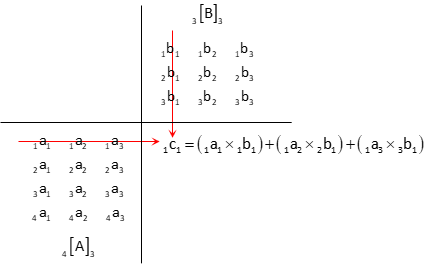
An easy way to visualize this is to arrange the first matrix so it is at lower left and the second at upper right:
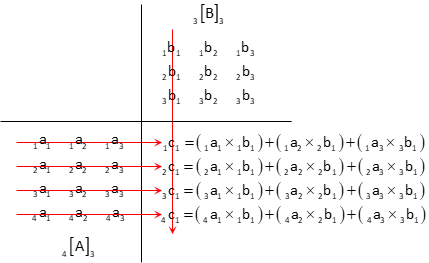
Then sum the products moving across A rows and down B columns
f. Inversion
An inverted matrix one which when multiplied by the original matrix results in an identity matrix. An inverted matrix is identified with a -1 superscript: the inverse of [A] is [A]-1.
[A] x [A]-1 = [I]
A matrix must be square and non-singular in order to be inverted, ||A|| < > 0.
There are a few ways to invert a matrix, depending on its size.
(1) By Determinant: can be used to invert a 2 x 2 matrix.
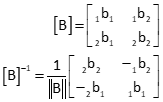
Example
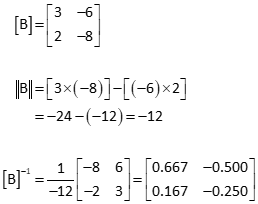
Check

(2) Method of Adjoints: can be used to invert a 3 x 3 matrix
This is a fairly involved process which requires determinants of nine 2 x 2 sub-matrices to create a co-factor matrix which is transposed and then multiplied by the determinant of the original matrix.... Because it is limited to 3 x 3 matrices, it's probably not worth memorizing unless you collect trivia.
(3) Row Manipulation: can be used to invert all square matrices.
Row manipulation starts with the matrix written left of an identity matrix. Rows of both matrices are multiplied, added, subtracted, etc, until an identity matrix is created on the left side. When that is accomplished, the matrix on the right is the inverse of the original matrix.
|
For example, to invert the matrix |
|
|
Place the identity matrix to its right |
|
|
Divide row 1 by 4 |
|
|
Multiply row 1 by 8, subtract it from row 2, and replace row 2 with the result |
|
|
Multiply row 1 by 5, subtract it from row 3, and replace row 3 with the result |
|
|
The first column on the left matrix matches the first column of an identity matrix. Note how the matrix on the right is changing. |
|
|
The matrix on the right is the inverse of the original matrix. |
|
|
The answer can be checked by [A] x [A]-1 = [I] |
|
(4) Diagonal Inverse
The inverse of a diagonal matrix is a second diagonal matrix with each element a reciprocal of its corresponding original matrix element.
|
The inverse of |
|
is |
|
|
|
which equals |
|
|