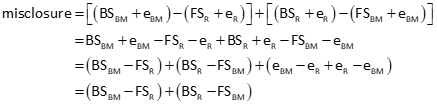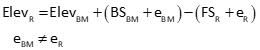2. Redundancy

a. Something Extra

When something is redundant, it is generally thought unnecessary. In a way, it is, but in measurement science, a redundancy is something extra that we try to give effect to. We routinely include extra measurements in surveying, for a few different reasons. Two are illustrated here with direct and indirect measurement examples.

b. Direct Measurement: Taping

Consider measuring a lot line once with a 100 ft steel tape. With the tape supported along its entire length and a carefully applied consistent 20 pound pull, the result is 362.24 ft. Can the length be reliably stated as 362.24 ft?

The distance is measured a second time, on a day colder by 25°F, with same support and pull, but this time the result is 262.19 ft. What happened? Did the distance actually shrink because of the temperature change?

If you have ever used a steel tape, you will immediately realize part of the problem: the number of full tape lengths was apparently miscounted. Either an extra full tape length was included in the first measurement or omitted from the second. Either way, a mistake was made. So how to resolve it? By measuring a third time and hoping it matches one of the first two.

If the third measurement is 362.36 ft, that means the second measurement has (at least) a full tape length mistake. We can either discard the second measurement or "correct" it by adding 100 ft. If we discard it, there's still a 0.12 ft difference between the first and last measurements. Much of this can be attributed to the temperature change which is a systematic error: the tape shrank at a lower temperature making the measurement too long. Once this and other systematic errors are compensated, the only errors left are random.

A single measurement of an unknown quantity is a unique solution - there is only one possible value for the unknown. Any measurement beyond the first is redundant. In this taping example, a second redundant measurement revealed a mistake existed, a third helped isolate it..

Should we automatically discard any measurements that contain a mistake? It could depend on the situation. In this example, assuming a tape mis-count happened, adding a full tape length makes the second measurement 362.19 ft which is consistent with the other two. Had it been 275.69 ft, an omitted 100 ft tape length doesn't account for the difference; something else happened. In either case, multiple measurements help identify where the mistake occurred. The safest thing to do is discard the mistaken measurement.

c. Indirect Measurement: Leveling

Let's look at the example of a simple differential level circuit. Elevations of points A and B are to be determined from a benchmark, BM Dog, Figure A-3.

Figure A-3 Leveling Circuit

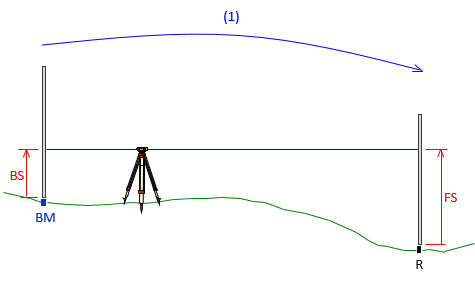
Differential leveling consists of a sequence of backsight (BS) and foresight (FS) rod readings, Figure A-4.

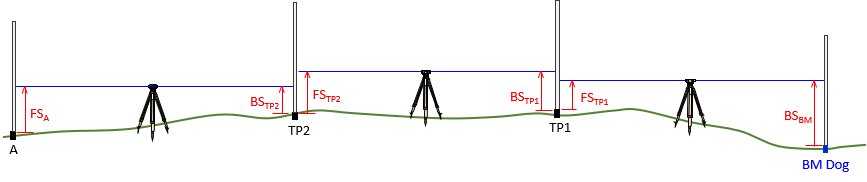Figure A-4 Differential Leveling

BS readings are added, FS subtracted to get the total elevation difference along a line, Equation A-4.

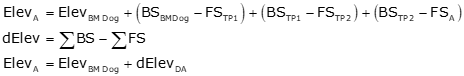Equation A-1 Equation A-2

In general terms, an observation is a measurement with which an unknown quantity can be determined. In this case specifically, it is the elevation difference dElev_DA from BM Dog to point A, Equation A-2. Because the intermediate points are temporary, dElev_DA is the sum of the FS readings subtracted from the sum of the BS readings, Equation A-1.

How many observations are necessary to determine the elevations of points A and B? Technically only two: one from BM Dog to A, another from A to B, Figure A-5.

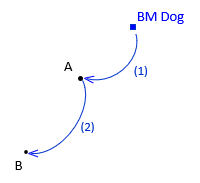Figure A-5 Connecting A to BM Dog

There are two unknown elevations and two measurements making this a unique solution. As with the taping example, the primary issue with a unique solution is insufficient information to determine if errors are present nor what kind they are. For example, a rod reading error would be undetectable. To address this, surveyors typically close a level circuit back to the original benchmark or another benchmark in the same vertical system, Figure A-6

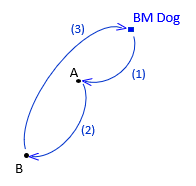Figure A-6 Closing the Circuit

This third observation back to the benchmark is a redundancy allowing misclosure determination. A redundancy is also called a Degree of Freedom (DF). The number of DF are determined from Equation A-3.

		Equation A-3
	DF: Number of degrees of freedom m: Number of observations n: Number of unknowns

DF must be equal to or greater than 0 or the unknowns cannot be solved. DF = 0 is a unique solution with no redundancy.
The sum of the three observations in Figure A-6 is the misclosure, its size depending on errors.

• A large difference indicates the presence of one or more mistakes.
• A smaller difference, but one outside some acceptable misclosure limit, could be the result of uncompensated systematic errors. For example, using a level with a collimation error and not balancing BS and FS distances.
• A small difference within an allowable misclosure limit is caused by random errors.

d. True or Pseudo Redundancies

Having redundancies alone is not sufficient, they must be the right kind. We can distinguish between true and pseudo redundancies.
To the circuit of Figure A-3, a third observation is added from A back to the benchmark., Figure A-7.

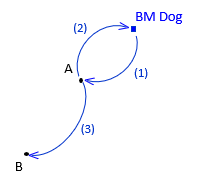Figure A-7 Pseudo Redundancy

There are two unknowns and three observations resulting in 3-2 = 1 DF. But point B is connected to point A with only one observation. Errors in that observation cannot be trapped. Even though we have one degree of freedom, it's for the section between BM Dog and point A so it isn't a true redundancy for the entire circuit. Another observation must be added connecting point B to the benchmark or to point A, Figure A-8.

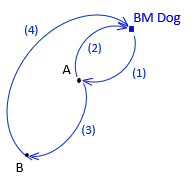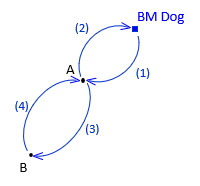(a) DF = 4-2 = 2	(b) DF = 4-2 = 2
Figure A-8 Redundancies Options

Each point must be connected to the network by at least two observations for true redundancy. More observations, more DF, Figure A-9.

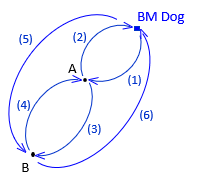Figure A-9 DF = 6-2 = 4

e. Independent Observations

Observations should be made independently of each other as much as possible to avoid repeating the same errors. Simply glancing away and then re-reading the instrument without changing anything does not constitute an independent measurement. A simple level loop between BM and point R, Figure A-10, has one redundancy.

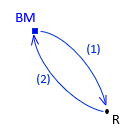Figure A-10 Simple Loop

In this case, the  surveyor had an unbalanced sight distance set up for the first observation, Figure A-9(a). After taking BS and FS readings, he left the instrument in place and simply reversed his readings, Figure A-11(b).

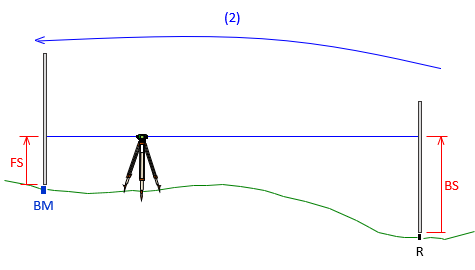Figure A-11 Simple Loop Observations

These are not independent observations. If the instrument had a collimation error, Figure A-12, there is an unresolved systematic error.

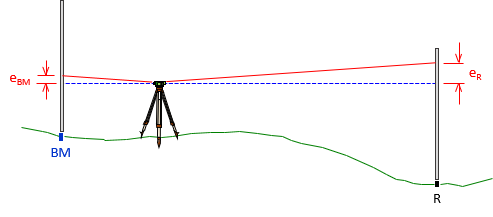Figure A-12 Collimation Error

The circuit would have a near perfect misclosure because both errors are added and subtracted so they cancel:

The only thing affecting misclosure are rod reading errors which are random.
Even though the misclosure may be acceptable, the elevation of point R is incorrect due to the collimation error:

Without independent observations (and correct field procedures) mistakes and systematic errors may not be found.