8. Example Computations
a. Atmospheric conditions
A distance of 846.39 ft was measured with no atmospheric correction applied by the instrument. What is the corrected distance if the temperature and atmospheric pressure were 85° and 29.2 in Hg?
Using Equation F-5:
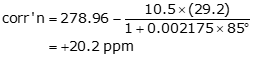
Applying the correction with Equation F-7:
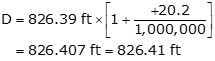
b. Slope reduction
The slope distance from a Section corner to a Quarter Section corner was measured as 2648.34 ft at a zenith angle of 92°14'20". What is the effect of earth curvature and refraction on the horizontal reduction?
The last term in Equation F-8 is the curvature and refraction correction for the horizontal distance. Use 14% for refraction and 20,906,000 ft for the earth's radius.
Solving the term for the conditions:

The zenith angle exceeds 90° which makes the correction negative. Because the correction is subtracted, the horizontal distance is actually longer than the slope distance in this situation.
c. Measurement Random Error
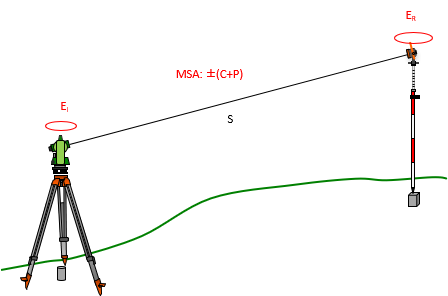
A total station's centering error over a point is ±0.005 ft, the reflector is mounted on a pole and its centering error is ±0.02 ft. The MSA for the instrument is ±(3mm + 4ppm). The distance measured is 753.84 ft. What is the expected random error in the distance?
Sketch:
The total random error in the distance comes from the Error of a Sum (refer back to Chapter F. Random Errors):
| Equation F-10 |
The constant and proportional part of the MSA are not independent errors. They are the expected uncertainty in a single measurement. When applying the Error of a Sum, the MSA is treated as a singular error.
| Equation F-11 | ||
|
Ei : Instrument centering error |
||
Compute MSA error components
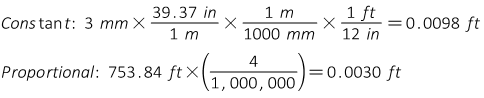
Use Equation F-11 to determine the expected error.
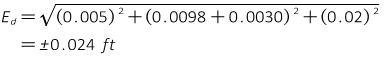
To further explore random error propagation, check the Distance and Angle Random Error Propagation spreadsheet in the Software section.