f. Vertical Circle Index
(1) Description
Reducing slope distance to horizontal requires measurement of a vertical or zenith angle. An index error exists if the vertical circle is not correctly oriented to gravity when the instrument is leveled. TSIs and most theodolites use a gravity actuated vertical circle which should orient itself automatically. Some earlier theodolites, particularly control quality instruments, had a separate bubble for vertical circle orientation. Those instruments types aren't addressed in this chapter.
(2) Check
Analog theodolites measure zenith angles; digital theodolites and TSIs can be set up to measure zenith or vertical (from the horizon) angles. We'll use zenith angles*****
Measure the Direct and Reverse zenith angles to a point and check their sum.
In Figure G-36 the Direct zenith angle is 70°.
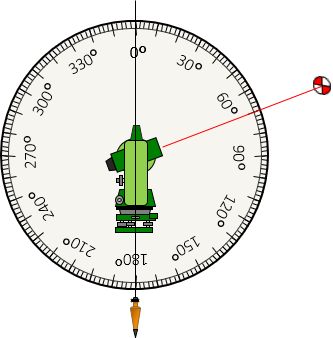 |
| Figure G-36 Direct Zenith Angle |
In Figure G-37 the Reverse zenith angle is 290°.
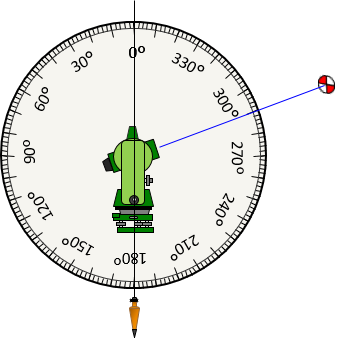 |
| Figure G-37 Reverse Zenith Angle |
Adding them: 290°+70°=360°
The sum of the Direct and Reverse angles should be 360°
What happens if the vertical circle is rotated 4°, for example?
The Direct zenith angle to the same point, Figure G-38, is 66°, 4° too small.
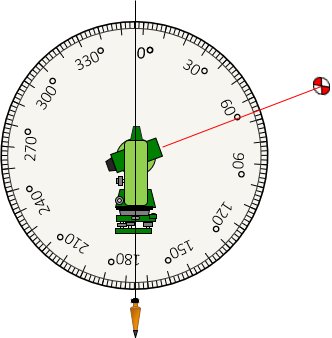 |
| Figure G-38 Direct Zenith Angle with Error |
The Reverse zenith angle, Figure G-39, is 286°, also 4° too small.
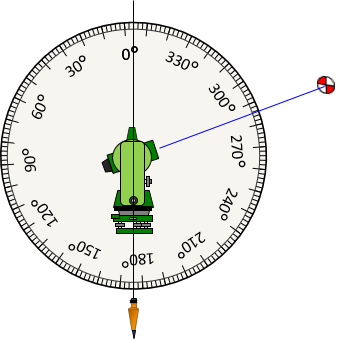 |
| Figure G-39 Reverse Zenith Angle with Error |
66°+286°=352°, which is 8° less than 360° and twice the circle rotation. Per Reversion Principle, the error is doubled.
(3) Compensation
(a) Procedure/Mathematical
Because a zenith angle is a continuous angle, the correct angle is not the direct and reverse average. Instead, an Index error is computed and applied to the measured zenith angle.
The Vertical Circle Index error is (360°-[ZD+ZR])/2. It is added to the direct (ZD) and/or reverse (ZR) angle.
For this example, the Index error is (360°-352°)/2 = +4°.
66°+4°=70° check
286°+4°=290° check
70°+290° = 360° check
(b) Adjustment
Neither a theodolite nor a TSI can be mechanically adjusted. Although a theodolite has a physical circle, it is not user accessible. A TSI uses a digital circle which can have 0° anywhere and axes compensation which should account for an index error. An error with either should be only be adjusted by a qualified repair facility