3. Grade

a. Definition

Grade is the slope of a straight line and is computed from:

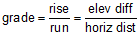	Equation A-1
elev diff: elevation difference horiz dist: horizontal distance

If the elev diff and horiz dist are both in feet (or meters) Equation A-1 results in grade as a dimensionless ratio; multiplying it by 100 converts it to a percentage (%).

If elev diff is feet and hori dist is stations, Equation A-1 returns grade as a percentage.

Grade is positive (+) going uphill in the direction of stationing, negative (-) going downhill, Figure A-7.

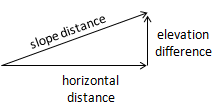Figure A-7 Grade

b. Examples

(1) The elevation at sta 10+25.00 is 1214.80 ft; at sta 12+75.00 it is 1193.50 ft.

What is the grade of the line between the two stations?

First, draw a sketch:

Using Equation A-1:

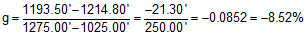
(2) At sta 16+50.00 the elevation is 867.50 ft. If the grade through 16+50.00 is +3.00%, what is the elevation at sta 19+00.00?

Sketch:

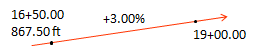
We need to rearrange Equation A-1 to solve for the elevation difference between the two stations:

The horizontal distance is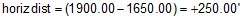
and elevation difference is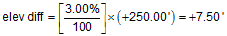
and elevation at 19+00.00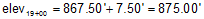

According to the sketch, 19+00 is higher than 16+50 so the computed elevation looks correct

(3) Using the data in example (2), what is the elevation at station 14+00?

Sketch:

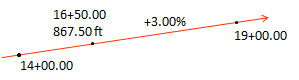
The horizontal distance is:

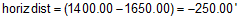
Since we're going backwards along the alignment, the distance is negative.

The elevation is:

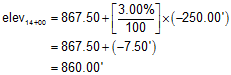
From the sketch we see that 14+00 is lower than 16+50, so the computed elevation looks correct.