A. Basic Components
1. Alignment
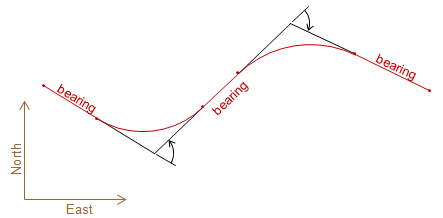
An alignment is a three dimensional refernce line consisting of a series of straight and curved segments. It serves as a reference for linear projects such as roads, pipelines, transmission lines, etc. Most alignments have horizontal and vertical components, Figures A-1 and A-2, each related but having their own geometric elements and specific design constraints.
 |
|
Figure A-1 |
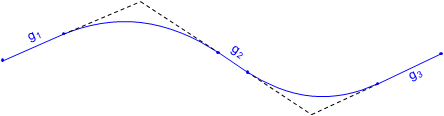 |
| Figure A-2 Vertical Component |
Although most contemporary alignment design is done digitally in three dimensions, it is still important to understand the geometry of the individual components.
The remainder of the chapter will concentrate on geometry for road alignments.
2. Stationing
A station is both a dimension and a position. As a dimension it has a fixed length with associated unit. As a position it is the cumulative horizontal distance along the alignment from its beginning.
In the English system, a station is defined as the length of a standard surveyor's tape making it 100.00 ft long. A position is expressed as the number of full stations (100 ft intervals) plus a partial station (less than 100 ft) and is written in the full+partial format. Station 8+35.67 is 835.67 feet along the alignment from its origin. Alignments do not usually start at station 0+00 because subsequent redesign can result in negative stations: -1+45.67 looks confusing, doesn't it?
For longer alignments and/or larger stationing values the 1000s format can be used. The number to the left of the + is the number of thousands of feet, to the right is the partial thousand: 2+987.35 corresponds to 2987.35 ft along the alignment.
In the metric system, a station may be 100 m or 1000 m with a corresponding partial station. A point 12,56.02 m along the alignment would be at station 12+26.02 or 1+256.02.
Alignments are traditionally staked at full station (100 ft) intervals, in the English system, and changes in horizontal direction, Figure A-3. In some cases, such as trenching, stakes can be placed at half- or quarter-station intervals (50 ft and 25 ft intervals, respectively).
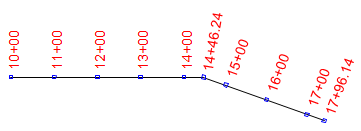 |
| Figure A-3 Stationing |
The horizontal distance between two stations along the alignment is their stationing difference.
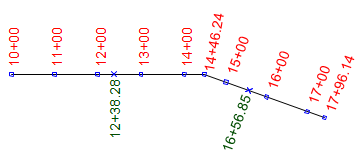 |
| Figure A-4 Distance |
In Figure A-4, the distance from sta 12+38.28 to sta 16+56.85 is:
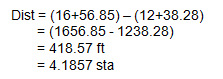
The distance can be expressed in feet or stations.
The position of a point off the alignment is expressed by a station and an offset to the right or left (defined looking upstation). The position of the CP in Figure A-5 is 11+68.26 82.40R
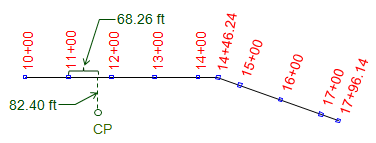 |
| Figure A-5 Station and Offset |
A single point can sometimes have two different stations values. The most common situation is where two different alignments cross, Figure A-6.
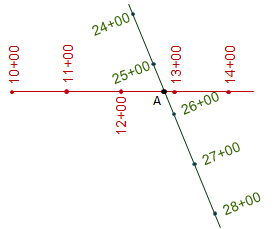 |
| Figure A-6 Station Equation |
Point A is at station 12+83 along one alignment and station 26+45 along a second. A Station Equation can be written for point A: Sta 12+83 = Sta 26+45. This may be brought to the readers' attention on a set of plans to ensure the appropriate station value be used for alignment calulations. Another station equation situation can occur in horizontal curve computations and will be covered in that section.
3. Grade
a. Definition
Grade is the slope of a straight line and is computed from:
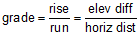 |
Equation A-1 |
| elev diff: elevation difference horiz dist: horizontal distance |
|
If the elev diff and horiz dist are both in feet (or meters) Equation A-1 results in grade as a dimensionless ratio; multiplying it by 100 converts it to a percentage (%).
If elev diff is feet and hori dist is stations, Equation A-1 returns grade as a percentage.
Grade is positive (+) going uphill in the direction of stationing, negative (-) going downhill, Figure A-7.
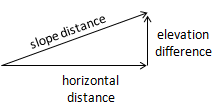 |
| Figure A-7 Grade |
b. Examples
(1) The elevation at sta 10+25.00 is 1214.80 ft; at sta 12+75.00 it is 1193.50 ft.
What is the grade of the line between the two stations?
First, draw a sketch:

Using Equation A-1:
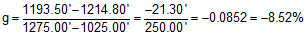
(2) At sta 16+50.00 the elevation is 867.50 ft. If the grade through 16+50.00 is +3.00%, what is the elevation at sta 19+00.00?
Sketch:
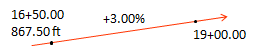
We need to rearrange Equation A-1 to solve for the elevation difference between the two stations:

| The horizontal distance is | 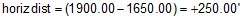 |
| and elevation difference is | 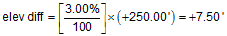 |
| and elevation at 19+00.00 | 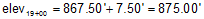 |
According to the sketch, 19+00 is higher than 16+50 so the computed elevation looks correct
(3) Using the data in example (2), what is the elevation at station 14+00?
Sketch:
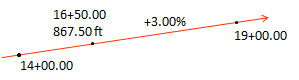
The horizontal distance is:
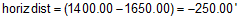
Since we're going backwards along the alignment, the distance is negative.
The elevation is:
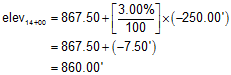
From the sketch we see that 14+00 is lower than 16+50, so the computed elevation looks correct.