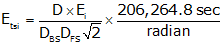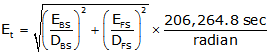4. Random Error Propagation
a. Combined Random Errors
(Much of the material in this section has been adapted from Chapter 6 of Adjustment and Computations, first edition, by Wolf & Ghilani).
Many surveyors presume the angle display resolution is the angle measuring accuracy of the TSI. For example, if the TSI display can be set to show angles to 1" then the angle measuring accuracy must be 1". This is no different than a measuring a distance with a tape having a smallest division of 0.01 ft: because you can measure to 0.01 ft doesn't mean your measurement is accurate to 0.01 ft. Holding the 0 end of the tape over the mark will be subject to random error as will reading the tape. Propagating individual random errors will affect the error in the final measurement. Instrument resolution is but one of those errors.
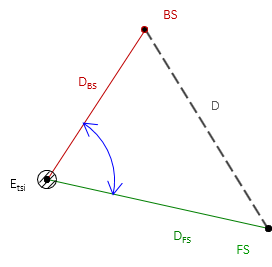
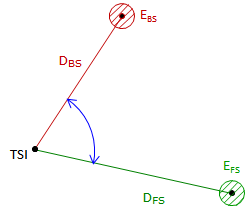
Random errors affecting an angle measurement are can be divided into three categories, Figure D-9:
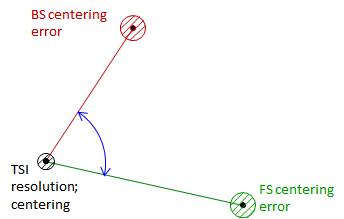 |
| Figure D-9 Centering and Sighting Errors |
(1) TSI Pointing and Reading error, Epr
This is a characteristic of the instrument itself much like the MSA for electronic distance measurement.
The DIN 18723 standard was developed as a way to express the expected angle uncertainty of a digital instrument. The standard is more a statement of precision rather than accuracy. A later parallel standard, ISO 17123:3, was developed for the same purpose as DIN 18723 but using different calibration criteria. Many instrument manufacturers have adopted the ISO standard in place of the DIN. The instrument manual should show one or the other in the TSI specifications.
The relationship between the DIN 18723 or ISO 17123:3 precision, EDIN, and the expected combined pointing & reading error in a measured angle, Epr, is:
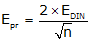 |
Equation D-1 |
EDIN and Epr are both in seconds of arc.
(2) TSI Centering error, Etsi
The error due to TSI centering is:
 |
|
||||
| Figure D-10 TSI Centering Error |
|||||
(3) Target Centering error, Et
 |
|
||||
| Figure D-11 Target Centering Errors |
|||||
(4) All Together...
The three errors are propagated as the Error of a Sum to determine the error in the measured angle:
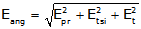 |
Equation D-4 |
(5) Examples
(a) Example 1
A TSI is used to measure an angle twice direct and reverse with a resulting average angle of 69°35'47". The BS mark is a tripod mounted target with a centering error of ±0.005 ft. The FS mark is a handheld prism pole. The bottom half of the pole is not visible because of the terrain so a centering error of ±0.02 ft will be used. The TSI has a 01" display and its centering error is ±0.003 ft. From the instrument manual, the TSI's stated ISO 17123:3 angle uncertainty is ±06". Approximate horizontal distances to site marks are shown in Figure D-12.
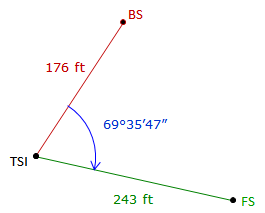 |
| Figure D-12 Example 1 |
What is the expected error in the measured angle?
TSI Pointing and Reading error
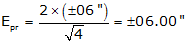
TSI Centering error
To determine this error we need the distance between the targets. This can be computed from the Law of Cosines using the measured angle and distances to the target:
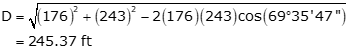
then
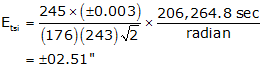
Target Centering error
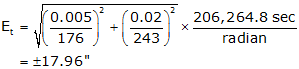
Combined
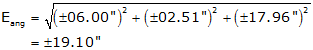
The expected error in the angle is ±0°00'19"
Analysis
What's the largest source of error? Target centering, the prism pole in particular, is the largest error contributor.
If we replace the pole with a mark similar to that of the BS, the target centering error drops to ±07.23" and expected angular error to ±00°00'10."
(b) Example 2
The angle shown in Fig D-13 will be measured with a TSI having an ISO 17123:3 angle uncertainty of ±05" and centering error of ±0.003 ft. Both BS and FS marks are tripod mounted, also with a centering error of ±0.003 ft.
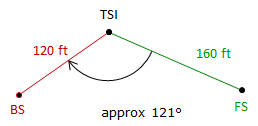 |
| Figure D-13 Example 2 |
How many D/R sets must be turned to achieve an expected angular error no greater than ±09"?
The only error affected by the number of angles turned is TSI Pointing and Reading, Equation D-1. After substituting TSI Centering and Target Centering errors in Equation D-4, it should be solved for the TSI Pointing and Pointing error. Equation D-1 can then be solved for n.
Compute TSI Centering error, Etsi
Compute distance between targets
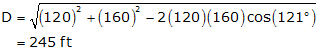
compute the error
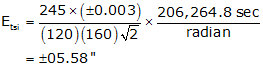
Compute Target Centering error, Et
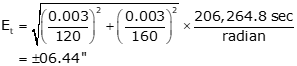
Set up Equation D-4 and solve for n
![]()
Square both sides, sort terms, and replace Epr with Equation D-1.
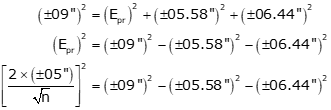
solve for n:
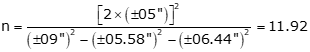
11.92 is the minimum value for n to achieve an expected accuracy of ±09"
n is the number of times the angle is measured, direct or reverse. Since we always measure direct and reverse sets, n must be an even integer. Since it's not possible to measure 11.92/2 = 5.96 D/R sets, n must be 12 (6 D/R) or 10 (5 D/R).
For n=10, the angular error, Eang, is ±09.1", juuuust outside the criterion.
For n=12 the angular error is ±08.998"=±09.0".
To meet the ±09" criteria, measure 6 D/R
To further explore random error propagation, check the Distance and Angle Random Error Propagation spreadsheet in the Software section.
b. Angle repetition
Measuring the same entity multiple times allows random errors to compensate. Although they can never be entirely eliminated their effect can be lessened through repeated measurements. Measuring an angle direct and reverse is done to compensate for systematic instrumental errors not random errors. The average of a D/R set constitutes a single measurement; it's that resulting angle which has random errors. So to reduce random errors, we repeat D/R sets.
When measuring an angle, once the TSI and targets are set up, their centering error effects do not change during the measurement set. The only thing affecting the final error in the measured angle is the number of times the angle is measured. As seen in the analysis at the end of the second example problem, increasing the repetition from 3 D/R to 4 D/R reduces the expected error from 09.1" to 08.8".
If we vary the number of D/R sets in Equation D-1 we can see how it affects the TSI Pointing and Reading error. The chart in Figure D-13 shows the effect on TSI pointing and reading error as the number of repetitions is increased. Initially, there is a large accuracy improvement up to about 6 D/R. Once past 20 or so sets, additional measurements yield smaller error improvements.
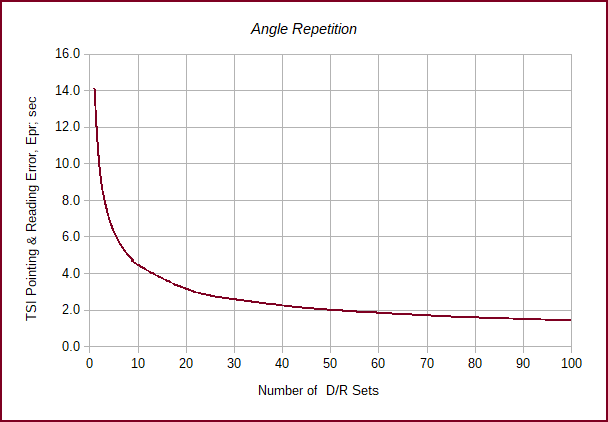 |
| Figure D-13 Angle Repetition Effect |
The chart in Figure D-14 compares three TSIs with different ISO angle uncertainties while varying D/R sets. At fewer D/R sets there is a larger error difference between the TSIs. As the number of D/R sets increase, the error differences become smaller.
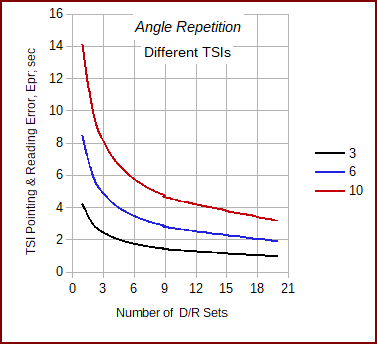 |
| Figure D-14 Different TSI Resolutions |
Figure D-14 can also be used to determine how many D/R sets are needed to meet a specific Epr. For example, to achieve a 4" accuracy:
- the 10" TSI would require 13-14 D/R sets
- the 6" TSI would require 4-5 sets
- the 3" TSI would require 1-2 sets
An example how this is applied is in the FGCC's Standards and Specifications for Geodetic Control Networks which contains a number of formal standards for angle measurement. In particular, the angle measurement standards for Precise Traverse include these two tables:
| Table D-2 Instrumentation Requirements | |||||
|---|---|---|---|---|---|
| Order | First | Second | Second | Third | Third |
| Class | I | II | I | II | |
|
Theodolite, least count |
0.2" |
1.0" |
1.0" |
1.0" |
1.0" |
| Table D-3 Field Procedures (partial) | |||||
|---|---|---|---|---|---|
| Order | First | Second | Second | Third | Third |
| Class | I | II | I | II | |
| Directions | |||||
|
Number of positions |
16 |
8 or 12† |
6 or 8* |
4 |
2 |
|
Standard deviation of mean not to exceed |
0.4" |
0.5" |
0.8" |
1.2" |
2.0" |
|
Rejection limit from the mean. |
4" |
5" |
5" |
5" |
5" |
|
† 8 if 0.2", 12 if 1.0" resolution. |
|||||
(A position is a single D/R set).
The least count in Table D-2 is actually the theodolite reading resolution. Although not the same as the DIN or ISO standard for digital equipment, least count was typically used for the same purposes until the 1980s (the last reprint of the Standards was in 1984).
Table D-3 contains similar information we divined from Figure D-14 except it includes a bit more detail. It formally identifies the number of D/R sets needed along with some variations based on equipment resolution. As a point of interest, note the night time observation requirement.
Keep in mind that this discussion and Figures D-13 and D-14 address only the TSI Pointing and Reading error. The total expected angle error would also include the TSI Centering and Target Centering errors which are independent of angle repetition.
c. Random Thoughts
So what does all this mean?
Because there are so many random error sources in measuring angles we have to be careful with measurement procedure. While equipment quality can make a difference in angular accuracy, it is only a single contributor. Equipment centering at all three points (BS, Occupied, FS). target types, and number of measurements all affect the quality of the final result. The discussion and examples in this chapter should provide the surveyor with a picture of how different errors can affect angular accuracy and what steps can be taken to minimize them.