Chapter G. The North American Horizontal Datum
1. History
The evolution of the North American datum is interesting, a bit convoluted, and a continuing process. Expansion of the spatial data user community and more accurate measurement technology increases pressure on the control network to meet ever greater accuracy needs. What used to take decades between datum refinements is reduced to years.
This chapter highlights major events in the North American datum history. For greater detail, the reader is directed to reference list included in Chapter A.
Note: Click any map to see a larger version
New England Datum - 1879
- Network: Along Eastern Coast and in Northeastern states
- Ellipsoid: Clarke 1899
- Origin: Control station Principio in Maryland
US Standard Datum - 1901
- Network: Extended network south and west; later added Transcontinental and Pacific arcs, Figure G-1
- Approximately 5,000 control stations
- Ellipsoid: Clarke 1866
- Origin: Meades Ranch in Kansas, Figure G-2, is identified as the origin but its position was computed from Principio; Azimuth to point Waldo fixed orientation.
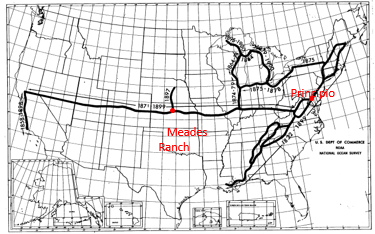 |
| Figure G-1 Control Network in 1901 “A Potpourri of Geodetic and Other Surveying Items”, Joseph F. Dracup Presented at the WSLS Annual Institute Jan 1977 |
 |
| Figure G-2 Control Station Meades Ranch NGS Photograph Archives |
North American Datum - 1913
- Canada and Mexico agree to tie their networks to the network. To reflect this, the US Standard Datum renamed the North American Datum. Nothing else changed.
North America Datum of 1927 (NAD 27) - 1932
- Network: 1901 US network expanded, Figure G-3; Canadian and Mexican networks added.
- Approximately 25,000 control stations
- Ellipsoid: Clarke 1866
- Origin: Control station Meades Ranch (as computed from Principio); Azimuth to Waldo
- Adjustment completed in 1932
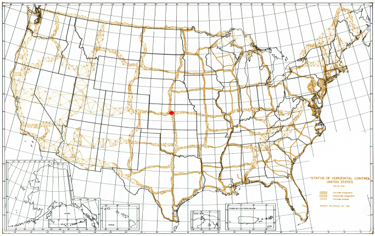 |
| Figure G-3 NAD 1927 Network “North American Datum of 1983”, Charles R. Schwartz, Editor, NOAA Professional Paper NOS 2, Dec 1989 |
North America Datum of 1983 (NAD 83) - 1986
- Network: Fifty years worth of additional densification, Figures G-4 and G-5
- Approximately 272,000 control stations
- Ellipsoid: Geodetic Reference System of 1980 (GRS 80)
- Origin: Geocentric fit
- Adjustment completed in 1986
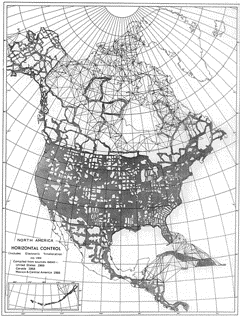 |
| Figure G-4 North American Control Network in 1969 “North American Datum” National Academy of Sciences, 1971 |
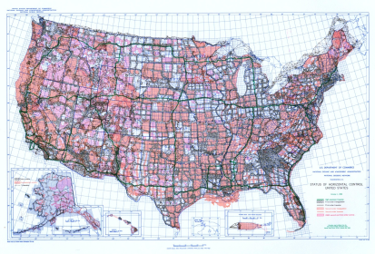 |
| Figure G-5 NAD 1983 Network NGS Website |
2. Paradigm Shift
a. What happened in 1983?
Up though NAD 27, the Clarke 1866 ellipsoid was used and regionally fit. At time of the adjustment, the network contained approximately 25,000 control stations. Because there were two unknowns for each station (latitude and longitude), an adjustment would require solving around 50,000 simultaneous equations. Consider the state of computing technology in the late 1920s and the challenge this posed. Dr. William Bowie, Division of Geodesy chief at the time, devised a method to partitioned the data into smaller sections for adjustment. For an explanation of the Bowie Method, see Chapter 2 of NOAA NOS Professional Paper 02 "North American Datum of 1983". The document is available in the Publications section of the NGS website.
By the 1980s, the number of control stations had increased by an order of magnitude. There was pressure on two fronts to update NAD:
- Control station accuracy was based on technology available before the 1932 adjustment. The following 50 years saw the evolution of measuring platforms which achieved accuracies higher than was in the network. Better measurements had to be degraded to fit the existing control.
- Satellite based platforms along with VLBI (Very Long Baseline Interferometry) allowed networks to extend beyond regional boundaries. A redesigned and geocentric ellipsoid would be a better global model.
- Better geoid modelling was possible because of increased measurement accuracy and computing capability.
It was decided that the best approach was a redefinition (different ellipsoid and fit) and readjustment to create a new datum.
The process started in the mid 1970s with a target completion date of 1983. Paper based measurements records had to be verified and hand coded (this was before scanners) and database management systems designed from scratch. Additional fieldwork was required to strengthen network geometry or replace lower quality measurements. With 270,000 stations (540,000 simultaneous equations) it was estimated that rounding errors would be an issue even with the available state-of-the-art mainframe computers ("Prediction of Roundoff Errors", Peter Meissi, ASCM Bulletin, No. 60, Feb 1978). That the completion date was missed by only three years is understandable.
b. Ellipsoids
Table G-1 shows the ellipsoids and their defined parameters used for NAD 27 and NAD 83.
| Table G-1 NAD Ellipsoids |
|||
| NAD | Ellipsoid | Fit | Fixed parameters |
| 27 | Clarke 1866 | North America | a = 6,378,206.4 m b = 6,356,583.8 m |
| 83 | GRS 80 | Global | a = 6,378,137 m 1/f = 298.25722 21008 8 |
c. How much did positions change?
Figure G-6 shows the final position shifts from NAD 27 to NAD 83 for CONUS.
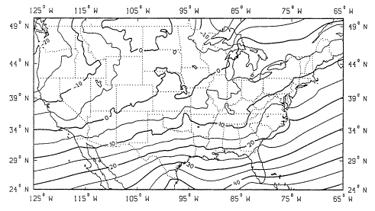 |
| (a) Latitude, meters |
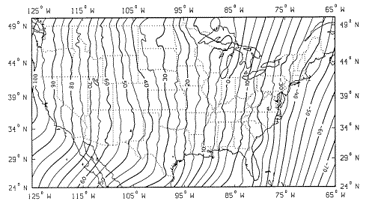 |
| (b) Longitude |
| Figure G-6 Position Shifts, NAD 27 to NAD 83 “North American Datum of 1983”, Charles R. Schwartz, Editor, NOAA Professional Paper NOS 2, Dec 1989 |
In the Aleutian Islands latitude and longitude shifts were as much as -160 m.
One of the greatest challenges in NAD 83 adoption was converting NAD 27 positions without introducing unacceptable errors. The shift maps show there was no uniform latitude or longitude change between the datums. NGS developed conversion software but it was understood that, at best, they provided only mapping quality positions.
3. So We're Done, Right?
The Global Positioning System not a production system at the time NAD 83 was being developed. The satellite constellation was sparse, receivers rare and expensive, and usable observation windows short. GPS observations (except for a literal handful) were not included in the NAD 83 adjustment.
Wisconsin's Department of Transportation (WIDOT) was an early adopter of GPS. After NAD 83 completion, WIDOT measured GPS baselines between adjusted control stations. First order points from different triangulation chains were used to compare computed with measured baselines. WIDOT found that the GPS baselines were more accurate than the control network. As with NAD 27, accurate GPS measurement would have to be degraded to fit the less accurate NAD 83 control network. WIDOT decided to densify the state's control network, measure it with GPS, and readjust it to NAD 83. Competed in 1991, the network was named the Wisconsin HPGN (High Precision Geodetic Network), Figure G-7.
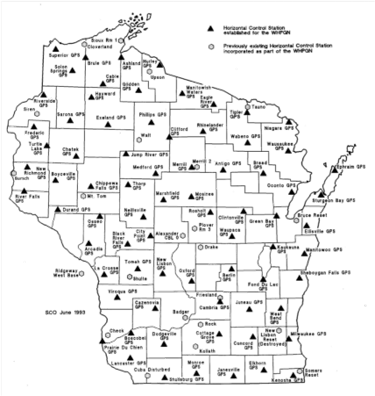 |
| Figure G-7 Wisconsin HPGN |
Because it was a readjustment of the NAD 83, it was referred to as NAD 83 (91) and the original as NAD 83 (86). Over time, aditional stations were added or replaced and parts of the network remeasured. The entire network was readjusted in 1997 creating NAD 83 (97). In the meantime, Minnesota did something similar and readjusted their network in 1996 creating NAD 83 (96).
See where this is headed?
More states began densifying, measuring, and readjusting their own networks creating state HARNs (High Accuracy Reference Networks). A problem caused by individual HARNs was where they abutted to other state networks. Because they were individually readjusted, there were inconsistencies across the networks.
When enough states had created individual HARNs, NGS decided to incorporate them all into a single readjustment. This became NAD 83 (NSRS2007). Part of this adjustment involved removing older lower quality measurements. The network was readjusted again creating NAD 83 (NSRS2011) with emphasis on GPS measurements. Many stations measured with only older conventional technology were not included in this readjustment. Each readjustment is a refinement of NAD 83, not a new datum.
Positions between readjustments did change, but not as significantly as the NAD 27 to NAD 83 (86) changes. Table G-2 shows the average position shifts in meters between readjustments in Wisconsin. The biggest change is from NAD 27 to NAD 83 (96). Subsequent changes were considerably smaller.
| Table G-2 Position Shifts in Wis |
||
| Shift | North (m) | East (m) |
| NAD 27 to NAD 83 (86) | -2.231 | -9.987 |
| NAD 83 (86) to NAD 83 (91) | +0.155 | +0.057 |
| NAD 83 (91) to NAD 83 (97) | +0.014 | -0.029 |
| NAD 83 (97) to NAD 83 (2007) | 0.000 | +0.008 |
| NAD 83 (2007) to NAD 83 (2011) | -0.002 | +0.018 |
Each datum readjustment is referred to as a datum realization. Not all control stations were included in all realizations. Stations only with older less accurate measurements were removed and more GPS-based stations added to maintain reference network integrity.
NGS is replacing NAD 83 and NAVD 88 with the North American Terrestrial Reference Frame of 2022 (NATRF2022) and North American-Pacific Geopotential Datum of 2022 (NAPGD2022). These were origianlly scheduled to be completed in 2022 but, in keeping with previous new datums, delays have pushed back completion. More information is on NGS' New Datums page.
Stay tuned...
4. Now What?
a. Who Uses the Horizontal Datum?
Quite simply, anyone who uses spatial data. To allow integration with other data, spatial data are based on formal coordinate systems. Formal coordinate systems are derived form a mathematical Earth model - a datum.
Even on small area projects, surveyors employing GPS are dependent on the datum:
- Whether calibrating to a formal coordinate system or local one, satellites are in the TRS and measured positions are converted to the end-user system. The TCS is based on the ellipsoid.
- GPS measures geodetic heights of ground points. A geoid height must be accounted for to determine orthometric height. The geoid and ellipsoid are integral parts of the horizontal datum.
b. Formal coordinate systems
The most obvious datum-dependent product is a formal coordinate system. Despite being unfamiliar with surveying or geodetic concepts, users are comfortable working with coordinate systems. For most, coordinate systems are transparent. All the user has to do is specify the project coordinate system, all the "messy" stuff is handled by software
Designing a coordinate system requires choices be made about distortions. What kind are there? How do they behave? How large is tolerable? Can they be computationally minimized or eliminated? There are many formal coordinate systems based on different needs and acceptable distortion levels.
The Horizontal Coordinate Systems topic describes how a grid coordinate system is designed, tied to the datum, and converting surveying measurements to/from of them.