Chapter F. Ellipsoid Fitting

1. Type of Fits

Because measurements are referenced to the geoid, an ellipsoid is selected and fit to it. The geoid is irregular (and changes over time) so no single ellipsoid fits it perfectly. Fitting an ellipsoid requires some degree of compromise.

a. Regional Fit

One approach is to fit an ellipsoid to a specific region of the geoid. Figure F-1.

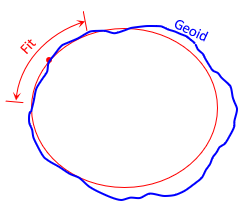Figure F-1 Regional Ellipsoid Fit

A point located centrally in the region is used as the fit origin. The ellipsoid and geoid coincide at this point - they are parallel  with no vertical separation between them. Parameters that are fixed are:

• Fit origins geodetic latitude and longitude
• Azimuth of a line from the origin point
• Two ellipsoid parameters

Making the geoid and ellipsoid coincide assumes the two surfaces do not separate significantly throughout the area. This was a reasonable assumption for an early datum definition before a good mathematical geoid model was available. The error introduced wasn't significant for most surveys.

Different regions would use their own ellipsoid sizes and fits to meet their needs, Figure F-2.

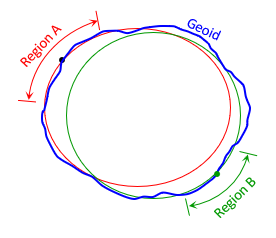Figure F-2 Multiple Fits

Of course, what fit one area wouldn't fit well anywhere else. That was of little consequence before global measurements were possible.

b. Global fit

Evolution of global measurement systems required developing models that weren't limited to regions. A geocentric ellipsoid, Figure F-3, was needed.

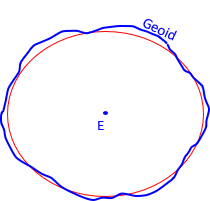Figure F-3 Geocentric Fit

The ellipsoid is fit by:

• Setting ellipsoid center at Earth's mass center
• Fixing orientation of the semi-major and -minor axes
• Specifying two geometric ellipsoid attributes