Chapter F. Ellipsoid Fitting

1. Type of Fits

Because measurements are referenced to the geoid, an ellipsoid is selected and fit to it. The geoid is irregular (and changes over time) so no single ellipsoid fits it perfectly. Fitting an ellipsoid requires some degree of compromise.

a. Regional Fit

One approach is to fit an ellipsoid to a specific region of the geoid. Figure F-1.

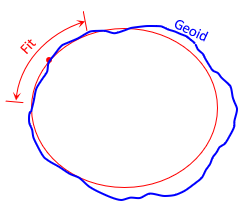Figure F-1 Regional Ellipsoid Fit

A point located centrally in the region is used as the fit origin. The ellipsoid and geoid coincide at this point - they are parallel  with no vertical separation between them. Parameters that are fixed are:

• Fit origins geodetic latitude and longitude
• Azimuth of a line from the origin point
• Two ellipsoid parameters

Making the geoid and ellipsoid coincide assumes the two surfaces do not separate significantly throughout the area. This was a reasonable assumption for an early datum definition before a good mathematical geoid model was available. The error introduced wasn't significant for most surveys.

Different regions would use their own ellipsoid sizes and fits to meet their needs, Figure F-2.

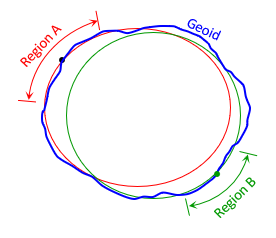Figure F-2 Multiple Fits

Of course, what fit one area wouldn't fit well anywhere else. That was of little consequence before global measurements were possible.

b. Global fit

Evolution of global measurement systems required developing models that weren't limited to regions. A geocentric ellipsoid, Figure F-3, was needed.

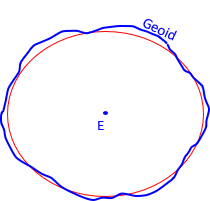Figure F-3 Geocentric Fit

The ellipsoid is fit by:

• Setting ellipsoid center at Earth's mass center
• Fixing orientation of the semi-major and -minor axes
• Specifying two geometric ellipsoid attributes

2. How Well Does it Fit?

Fitting a mathematical surface to a nonmathematical one means there will be varying skewness and separations between them. These are expressed by the Deflection of the Vertical and the Geoid Height both of which vary throughout the areas.

a. Deflection of the Vertical

The deflection of the vertical, δ, is the angle between the vertical line defined by gravity and the ellipsoid normal, Figure F-4. The ellipsoid normal lies in the meridian. Because the vertical line is defined by gravity, it is normal to the geoid so is not restricted to the meridian. 

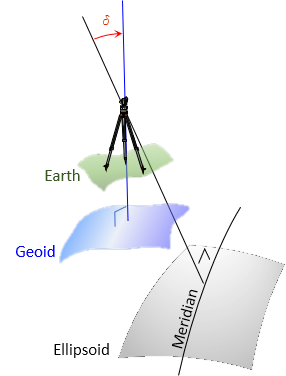Figure F-4 Deflection of the Vertical

The deflection is an indication of the skewness between the geoid and ellipsoid. If gravity and the ellipsoidal normal coincide, then the geoid and ellipsoid are parallel.

Components

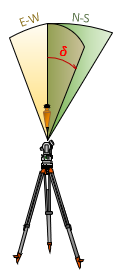
The deflection in the vertical is divided into two components: one in the N-S meridian (ξ) and the other perpendicular to it in the E-W direction (η), Figure F-5.

(a)	(b)	(c)
Figure F-5 Separation into N-S and E-W Components

Celestial Observations

Prior to GPS it was common to perform a celestial observation to establish direction for a survey.  Either the Sun or Polaris was sighted and the time recorded. Then using a star ephemeris, the direction of the sighted body could be determined.

The observer's latitude could be determined, just like ship navigator using a sextant. Recall in spherical coordinates we identified two types of latitude: geocentric and geodetic. Geocentric is with respect to the ellipsoid center; geodetic the ellipsoid normal. Astronomic latitude, ω, is a third and it is with respect to gravity, Figure F-6.

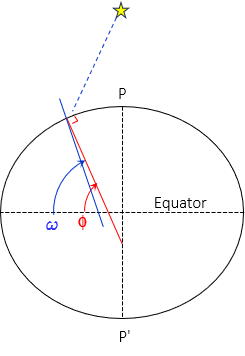Figure F-6 Astronomic Latitude

Equations F-1, -2, and -3 relate geodetic position and direction to astronomic ones using the deflection of the vertical's components.

	Equation F-1
	Equation F-2
	Equation F-3

The last term in Equation F-3 is known as the LaPlace Correction.

b. Heights

Unless the ellipsoid is made to coincide with the geoid, separations between the surfaces vary, Figure F-6.

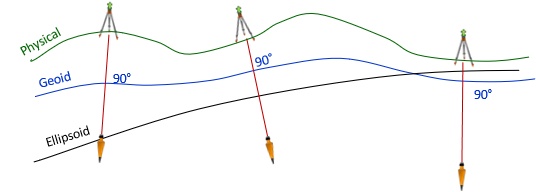Figure F-6 Surface Separations

There are three heights at each point, Figure F-7:

• H: Orthometric height; from the geoid to the ground point; elevation determined by leveling from a benchmark. The orthometric height is independent of the ellipsoid used to model the geoid.
• N: Geoid height; from the ellipsoid to the geoid. Also known as the geoidal height.
• h: Geodetic height; from the ellipsoid to the ground point. Also known as the ellipsoidal height.

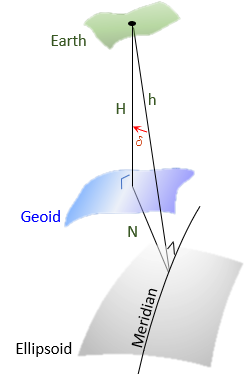Figure F-7 Heights

The heights are approximately related by Equation F-4.

Equation F-4

This is a close approximation because the deflection of the vertical, δ,  is relatively small and the geoid height is generally much smaller than the ellipsoidal height.