2. Geoid

According to the Geodetic Glossary, a geoid is:

"The equipotential surface of the Earth’s gravity field which best fits, in the least squares sense, mean sea level"

Equipotential means equal energy. Picture a lake's still surface on a calm windless day; because water can flow the still surface represents balanced forces - it is an equipotential surface. Theoretically the geoid is the equipotential surface represented by the seas, hence Mean Sea Level (MSL). The two primary forces which are balanced are gravitational and centrifugal. 

a. Gravitational Force

Gravitational force, which pulls inward, is a function of mass. The earth is not a homogeneous solid, it has layers, mass anomalies, and a shifting molten interior. Instead of straight radial lines pointing to a single center point, gravitational lines curve and deviate based on mass distribution, Figure B-5. They are neither straight nor converge to a singular point.

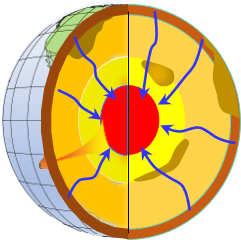Figure B-5 Gravitational Force

b. Centrifugal Force

Centrifugal force, Figure B-6, is caused by the earth's rotation and pushes outward. The further the surface is from the rotational axis, the greater the centrifugal force. It is greatest at the equator diminishing to zero at the poles.

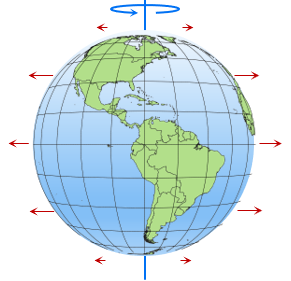Figure B-6 Centrifugal Force

This tends to make the geoid, and Earth, bulge at the Equator and flatten at the poles. 

 Forces affecting the geoid are a little more complex than that, but these two forces will suffice for now.

c. Geoid Shape

Gravity is the combined effects of gravity and centrifugal force and define the geoid. Because of earth's internal dynamics, external forces (eg. Moon), wobble as it spins, etc, the geoid is not uniform, Figure B-7, and changes over time. The geoid is smoother than the physical earth, but it is not a mathematical surface. Measurements made with ever more sophisticated equipment facilitates better modeling. NGS continually updates the geoid model and makes the information available to users and software developers.

(Wait a sec: if the geoid is non-mathematical, then how can NGS model it? For that we need a mathematical reference system, something we're building up to, so please be patient a bit longer.)

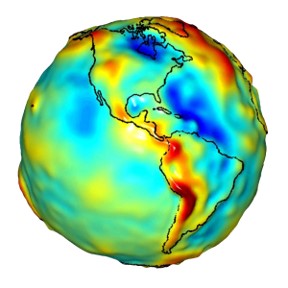Figure B-7 Geoid (NASA/JPL CA Inst Tech)

Most surveyors weren't really aware of the geoid as a surface importance prior to the initial NAD 1983 horizontal datum readjustment (this will be discussed in greater depth in later chapter). Although not aware of the geoid as a concept, surveyors all the way back to the Egyptian rope stretchers depended on it. When we set up equipment by centering a bubble or suspending a plumb bob, we are referencing ourselves to the geoid. We can't see it or kick it, but it's there; always has been, always will be.

A freely suspended plumb bob is a visual indication of the gravity vector at an instrument location. The gravity vector is perpendicular to the geoid, Figure B-8.

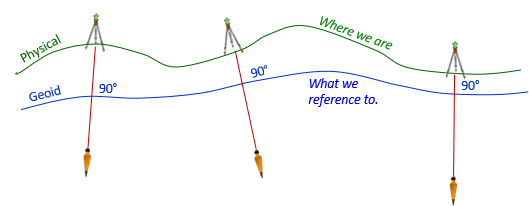Figure B-8 Earth and Geoid

Because the geoid is irregular, gravity vectors aren't uniformly radial extending to the Earth's center. This complicates creating a mathematical model of the Earth, but the more we know about the geoid, the better we can relate it to the physical surface and build spatial reference systems. And those start with a datum.