J. Reduction Example: Survey & Control
1. General
To fit a grid system, most surveying measurements will need modification to account for projection distortion. Depending on the survey purpose and quality, computations may be simple or involved
To reduce measurements, it is necessary to know
| distance: | elevation, geoid height, grid scale |
| direction: | convergence |
| angle: | false easting (Eo, cylindric) or false northing (No, conic) |
A survey must be connected to at least one known control point, from whose datasheet most of this data can be extracted. Others data may require software, like NGS's NCAT.
This chapter will introduce some survey data and control information. Chapter K will show measurement reduction for a conic SPC system, Chapter L for a cylindric UTM system.
2. Survey Data
Figure J-1 shows measurement data for the example.
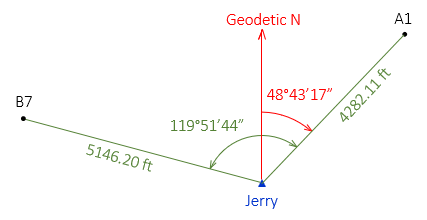 |
| Figure J-1 Survey Data |
The elevations of points A1 and B7 scaled from a topoquad are 1085 ft and 1340 ft, respectively.
3. Control Data
Jerry, Figure J-2, is NSRS control point NH0936 set in 1983 (by yours truly) as part of the first GPS network in Wisconsin.
 |
| Figure J-2 Jerry |
Figure J-3 is geodetic and grid data from Jerry's NSRS datasheet.
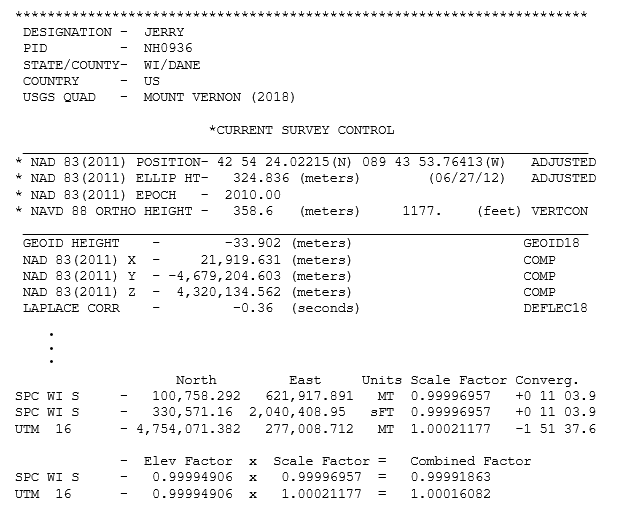 |
| Figure J-3 Jerry Spatial Data |
Jerry was included in the NAD 83 (2011) adjustment and has grid coordinates in:
Wis South SPC zone - Lambert conic projection; survey feet (sFT) and meters (MT)
UTM 16 - Transverse Mercator cylindric projection; meters (MT)
Scale Factors and Convergences differ for SPC and UTM since they are two different grid systems. The Elevation Factor is the same because it represents distance distortion from Jerry's elevation to the ellipsoid which is grid-independent.