D. Stereovision

1. Not Seeing Double 

Stereophotography allows us to obtain 3D information from 2D images. So how is that possible? Those of us with bi-cameral vision can see in 3D because we have two eyes separated by a nose (the nose is more than just a smelling organ). That means we see the same objects from two different perspectives: left and right. This is called stereovision. If you close one eye, your view is no longer 3D - you might think it still is, but your mind is used to "filling in the details" to interpret in 3D what your single eye sees in 2D.

Did you ever have a GAF Viewmaster ^TM as a kid? (I'm dating myself). It was a binocular-type device in which a round disk was inserted, Figure D-1.

(a) Viewer	(b) Image disk
Figure D-1 Viewmaster System

On opposite edges of the disk were paired slides of the same scene from slightly different perspectives. Looking through the Viewmaster eyepieces you would see a single 3D image. Each eye was forced to look at a different image.

Similarly, if you ever went to one of those horrid 3D movies, you were given a pair of cheap paper-frame glasses having one red lens and one blue lens, Figure D-2.

Figure D-2 3D Glasses

Wearing the glasses (supposedly) allowed seeing 3D movie effects.The movie was filmed simultaneously from two perspectives, with one camera using a red filter, the other blue. When viewing the movies with the glasses, the red-filtered eye was forced to see one image, the blue-filtered the other. Without the glasses, the movie looked blurry. Most of the time it didn't work too well because peoples' eye geometry and eyesight vary too much. 3D movies' biggest success was creating headaches. Using red and blue filters is known as an anaglyphic viewing system. A related system used polarized lenses with lens polarization 90° apart.

2. Stereograms

Figure D-3 shows optical geometry when viewing 3D objects. The sight line from each eye intersect the object forming a parallacrtic angle, Φ.

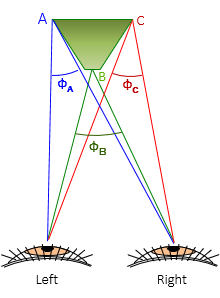Figure D-3 Parallactic Angles

Figure D-4 is a stereogram of the object viewed in Figure D-3. Each image of the stereogram represents what each eye sees.

Figure D-4 Stereogram

When each eye is forced to look at its own image, the object will appear in 3D. While looking at the image pair, relax your eyes until you see three images; concentrate on the middle one. You should see a truncated 3D pyramid.

(You may have to tilt your head a bit to line the images and they might be too close together if you're viewing on a smartphone.)

What happens if you close one eye?

Figure D-5 is shows stereograms of three different objects.
 

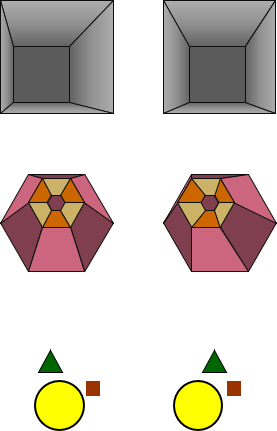Figure D-5 Stereograms

Try viewing each object in 3D. The last stereogram might be the hardest because it has three objects projecting at different heights. If you concentrate on the closer one, the farthest one may separate and vice versa. That's how our eyes normally operate: you can't focus on objects that are very close and very far away simultaneously.

The geometry of each image in the stereograms differ slightly, reflecting the two perspectives. Figure D-6 shows the images of the first Figure D-5 stereogram overlaid, the left in blue, the right in red.

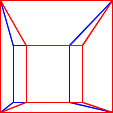Figure D-6 Overlaid Images

Though similar, the images are not identical. The bit of geometric difference is sufficient to support 3D viewing.

Figure D-6 is an anaglyphic stereogram, like the previously mentioned headache-inducing 3D movies; it will appear in 3D if you view it with anaglyphic glasses.

Hey, what happens if we force each eye to look at the opposite image? Figure D-7 are the first two stereograms from Figure D-5; the only difference is the left and right image of each pair are swapped.

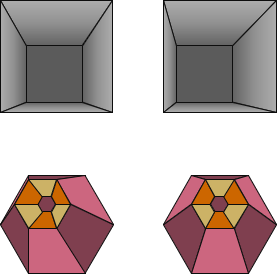Figure D-7 Swapped Images

When view stereoscopically, their geometry is reversed so the pit should look like a pillar and the column like a hole.

3. Stereoscopes

In photogrammetry, camera positions define the perspective positions, Figure D-8.

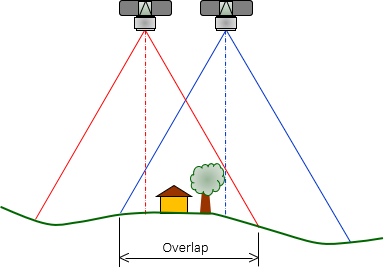Figure D-8 Aerial Photographs

To view the overlap as a 3D model requires the left eye looking at the left overlap area and the right eye the right. Photographs from mapping cameras are usually 9" x 9".

When placed side-by-side, the overlap is wider than the viewer's eye base. Laying one photo atop the other, Figure D-9, partially obscures the 3D view.

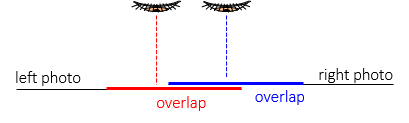Figure D-9 Obscured View

Not everyone is able to comfortably view two separate images simultaneously without an aid. A stereoscope is an instrument which makes viewing the 3D model easier. A basic  stereoscope has two eyepieces to aid each eye view a specific image, Figure D-10.

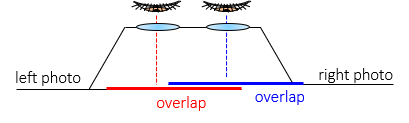Figure D-10 Basic Stereoscope

The eye base is unaltered so one photo must still be on top of the other.

A mirror stereoscope, Figure D-11, uses first-surface mirrors and right-angle prisms to allow wider photograph spacing.The entire 3D model can be viewed and measurements more easily made.

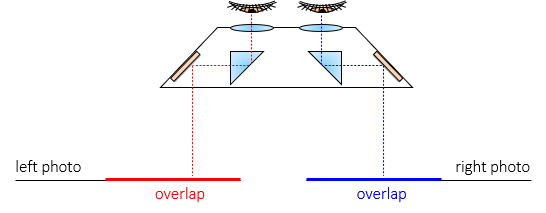Figure D-11 Mirror Stereoscope