2. Stereograms

Figure D-3 shows optical geometry when viewing 3D objects. The sight line from each eye intersect the object forming a parallacrtic angle, Φ.

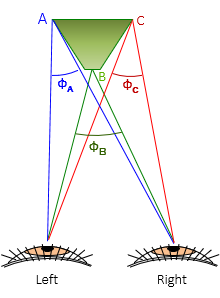Figure D-3 Parallactic Angles

Figure D-4 is a stereogram of the object viewed in Figure D-3. Each image of the stereogram represents what each eye sees.

Figure D-4 Stereogram

When each eye is forced to look at its own image, the object will appear in 3D. While looking at the image pair, relax your eyes until you see three images; concentrate on the middle one. You should see a truncated 3D pyramid.

(You may have to tilt your head a bit to line the images and they might be too close together if you're viewing on a smartphone.)

What happens if you close one eye?

Figure D-5 is shows stereograms of three different objects.
 

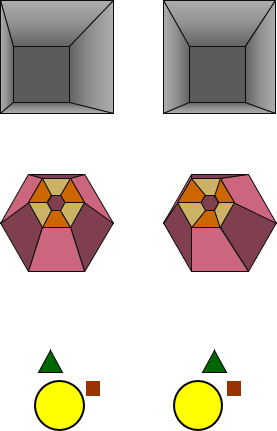Figure D-5 Stereograms

Try viewing each object in 3D. The last stereogram might be the hardest because it has three objects projecting at different heights. If you concentrate on the closer one, the farthest one may separate and vice versa. That's how our eyes normally operate: you can't focus on objects that are very close and very far away simultaneously.

The geometry of each image in the stereograms differ slightly, reflecting the two perspectives. Figure D-6 shows the images of the first Figure D-5 stereogram overlaid, the left in blue, the right in red.

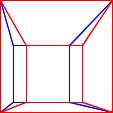Figure D-6 Overlaid Images

Though similar, the images are not identical. The bit of geometric difference is sufficient to support 3D viewing.

Figure D-6 is an anaglyphic stereogram, like the previously mentioned headache-inducing 3D movies; it will appear in 3D if you view it with anaglyphic glasses.

Hey, what happens if we force each eye to look at the opposite image? Figure D-7 are the first two stereograms from Figure D-5; the only difference is the left and right image of each pair are swapped.

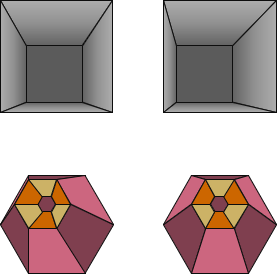Figure D-7 Swapped Images

When view stereoscopically, their geometry is reversed so the pit should look like a pillar and the column like a hole.