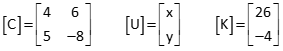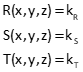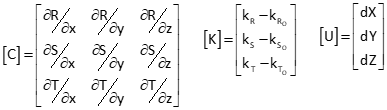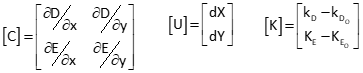D. Equations and Matrices
1. Linear Equations
a. Matrix Algorithms
A set of simultaneous linear equations can be denoted in matrix form as:
|
[C] x [U] = [K] |
Equation D-1 | |
|
[C]: Coefficients; this is a square matrix, n x n, because there are the same number of equations as unknowns. |
||
|
The three matrices for equations |
|
|
|
|
| are: |
|
To determine the values for the variables, the matrix expression must be solved for matrix [U]. The matrix algorithm to do so is:
|
[U]=[CTC]-1 x [CTK] |
Equation D-2 |
b. Example
Given the following equations, solve for x, y, and z using matrices.
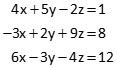
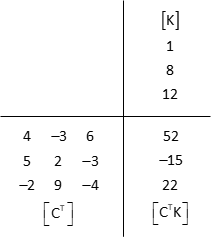
(1) Set up [C], [U], and [K] matrices
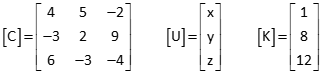
(2) Transpose [C]
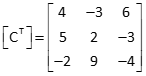
(3) Multiply [CT] and [C]
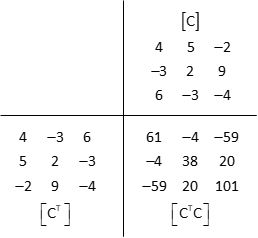
(4) Determine the inverse of [CTC]
Use Row Manipulation
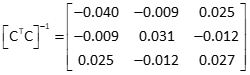
(5) Multiply [CT] and [K]
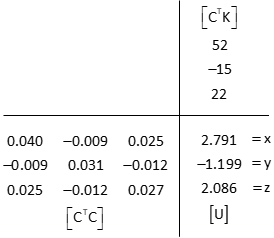
(6) Multiply [CTC]-1 and [CTK] to get [U]
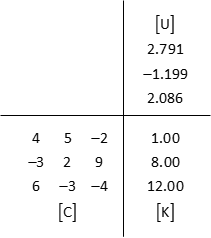
(7) Optional: check [K] = [C] x [U]
(8) Solution summary
x=2.791
y=-1.199
z=2.086
2. Non-Linear Equations
a. Matrix Algorithms; Matrix Structures
Simultaneous non-linear equations are solved using the abbreviated Taylor Series. This requires an iterative solution, beginning with approximations for the unknowns, and refining them until some correction criteria is met.
Equations D-1 and D-2 are used to set up and solve non-linear equations.
|
[C] x [U] = [K] |
Equation D-1 |
|
[U] = [CTC]-1 x [CTK] |
Equation D-2 |
Matrix elements are modified from their linear counterparts to incorporate the Taylor Series:
- Each [C] matrix element is a partial derivative of a function with respect to each variable evaluated at an approximation.
- Each [K] matrix element is the difference between the function's constant and that computed from approximations.
- The [U] matrix has corrections which are used to update the approximations.
|
For these three functions in three unknowns: |
|
|
|
|
|
The matrices are: |
|
|
|
|
After [U] is determined, its elements are used to update the approximations. The [C] and [K] matrices are recomputed and the process repeated until the corrections reach an acceptable level.
b. Example
Determine x and y values which satisfy these equations.
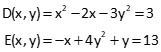
Start with initial approximations of x = 4 and y = 3. Continue until the corrections do not exceed 0.1.
This are the same equations used in the Chapter C's Taylor Series two variable example. Let’s see if we get the same answers.
(1) Matrix contents
|
|
(2) Partial derivatives with respect to each unknown
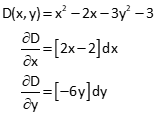
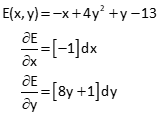
(3) First Iteration
Build [C] from partial derivative coefficients at the initial approximations
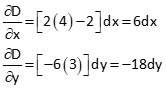
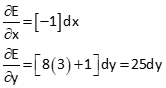
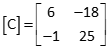
Compute expression constants at the initial approximations
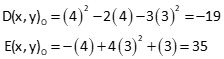
Compute [K] elements
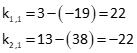
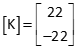
Transpose [C], then multiply [CT] by C.
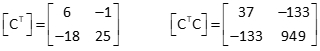
Determine the inverse of [CTC].
A 2 x 2 matrix can be inverted using the Determinant Method.

Multiply [CT] and [K].
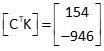
Determine [U] by multiplying [CTC]-1 and [CTK].
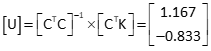
The corrections exceed 0.1 so continue with a second iteration.
(4) Second Iteration
Update initial approximations
x = 4+1.167 = 5.167
y = 3-0.833 = 2.167
Recompute [C] and [K] matrices
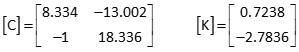
Compute [U] matrix

The corrections still exceed 0.1 so continue with a third iteration.
(5) Third Iteration
Updated approximations
x = 5.167-0.164 = 5.003
y = 2.167-0.161 = 2.006
Recompute [C] and [K] matrices
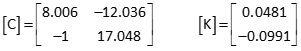
Compute [U] matrix
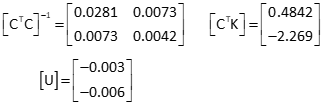
The corrections are less than 0.1 so the iterations can terminate.
(5) Final Values
x = 5.167-0.003 = 5.000
y = 2.006-0.006 = 2.000
These are the same as the example in Chapter C.
Ta-daa!
3. Software
Matrices provide a systematic approach to simultaneous equation solution. Although manual matrix computation can be lengthy, particularly matrix inversion, the process is easily programmed. Both these address the issues discussed at the end of Chapter C.
Although not as flexible as dedicated software, most spreadsheet programs have matrix functions. Table D-1 shows some functions in three different packages.
|
Table D-1 |
||
Function |
Microsoft Excel LibreOffice Calc |
Corel Quattro Pro |
| Transpose | =TRANSPOSE(array) | @TRANSPOSE(array) |
| Multiply | =MMULT(array1;array2) | @MMULT(array1,array2) |
| Inverse | =MINVERSE(array) | @MINVERSE(array) |
(inclusion of a particular program by name is not an endorsement of that particular product, although LibreOffice Calc is shareware so available at little to no cost)
The functions are similar in each but there some syntax differences.
In each, an array is designated by the cell addresses of the top left and bottom right array elements.
In Excel and Calc, the destination array's cells must be highlighted and the matrix function entered using Shift+Ctrl+Enter.
In Quatto Pro, the function is entered using Enter in the top left cell of the destination array.
As long as the spreadsheet is set to auto-recalcularion, destination arrays will update when any source array elements change. For an iterative solution, enter the initial approximations in specific cells and use them to set up the [C] and [K] arrays. After the matrix functions are set up correctly, the initial approximations can be updated using the [U] matrix values which in turn updates the rest.