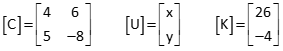Page 1 of 3
D. Equations and Matrices
1. Linear Equations
a. Matrix Algorithms
A set of simultaneous linear equations can be denoted in matrix form as:
|
[C] x [U] = [K] |
Equation D-1 | |
|
[C]: Coefficients; this is a square matrix, n x n, because there are the same number of equations as unknowns. |
||
|
The three matrices for equations |
|
|
|
|
| are: |
|
To determine the values for the variables, the matrix expression must be solved for matrix [U]. The matrix algorithm to do so is:
|
[U]=[CTC]-1 x [CTK] |
Equation D-2 |
b. Example
Given the following equations, solve for x, y, and z using matrices.
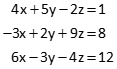
(1) Set up [C], [U], and [K] matrices
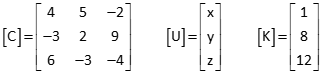
(2) Transpose [C]
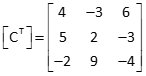
(3) Multiply [CT] and [C]
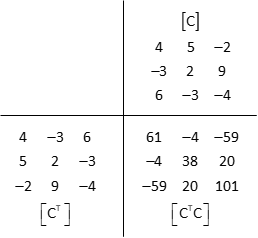
(4) Determine the inverse of [CTC]
Use Row Manipulation
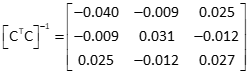
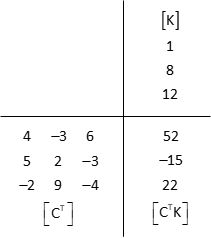
(5) Multiply [CT] and [K]
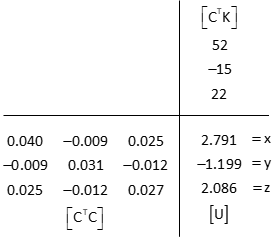
(6) Multiply [CTC]-1 and [CTK] to get [U]
(7) Optional: check [K] = [C] x [U]
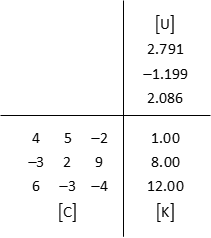
(8) Solution summary
x=2.791
y=-1.199
z=2.086