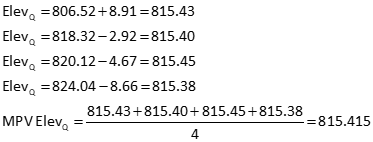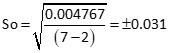B. Brute Force Method
1. General
Since the MPV is the value which meets the least squares criterion, why not compute every possible value of the each unknown and then average them? Depending on the number of observations and unknowns, this can involve a lot of computations. We can refer to this approach as the Brute Force method of LS adjustment.Will it work in all situations?
2. Level Circuit LS Adjustment
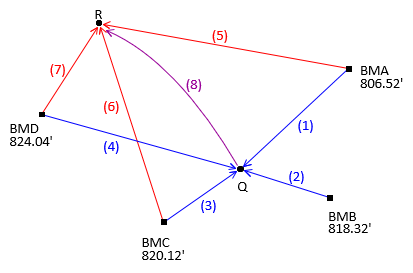
For the leveling circuit in Figure B-1
 |
| Figure B-1 Level Circuit |
and these observed elevation differences
| Obs | Line | dElev | Obs | Line | dElev | |
| 1 | BMA-Q | +8.91 | 5 | BMA-R | -3.56 | |
| 2 | BMB-Q | -2.92 | -- | -- | ||
| 3 | BMC-Q | -4.67 | 6 | BMC-R | -17.12 | |
| 4 | BMD-Q | -8.66 | 7 | BMD-R | -21.10 |
what are the elevations of points Q and R?
A traditional simple adjustment is difficult to apply in this situation. Because point Q is connected to four benchmarks and point R to three, any simple adjustment attempted will result in multiple elevations for each point.
With a small network like this, a Brute Force approach might be feasible. Using the observed elevation differences, compute all possible elevations for points Q and R, then simply average them.
Point Q elevations and their average are:
Similarly, for point R:
Compute So
Compute residuals using the adjusted elevations and the individually computed elevations used for the averages.
| v = MPVQ-ElevQ | v2 | sums |
| -0.015 | 0.000225 | |
| +0.015 | 0.000225 | |
| -0.035 | 0.001225 | |
| +0.035 | 0.001225 | 0.002900 |
| v = MPVR-ElevR | v2 | |
| +0.007 | 0.000049 | |
| -0.033 | 0.001089 | |
| +0.027 | 0.000729 | 0.001867 |
| 0.004767 |
There are seven observations (m) and two unknown elevations (n).
3. Will Brute Force Work in All Situations?
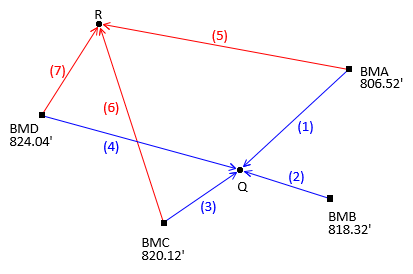
Add an observation, dElev(8)=-12.47, between points Q and R, Figure B-2.
|
|
| Figure B-2 Observation Added |
A fourth elevation for point R must be computed from point Q using the eighth observation. But which elevation of point Q should be used? Any of them? All of them? Its average?
The issue is more fundamental. When two unknowns are connected with a measurement, both are affected; after all, it's a network. Even though the observation is from point Q to point R, point Q's elevation is also affected. So point R's elevation depends on point Q's and point Q's elevation depends on point R's....
Adding another observation in the opposite direction from point R to point Q, Figure B-3, further complicates it.
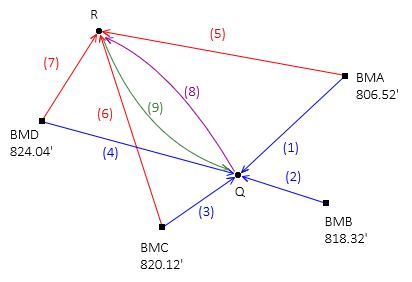 |
| Figure B-3 Another Observation Addition |
4. So Can We Use it?
Interconnections make for a stronger network, but Brute Force can't be used with them. Although the approach worked for the network in Figure B-2, the adjustment was actually two separate adjustments since neither point influenced the other.
Surveyors typically include redundant observations connecting the unknown points, whether a simple one dimension leveling network or two- and three-dimension surveys. Brute Force is too limited to be applied. A more systematic LS adjustment method allowing interconnected observations is needed.