3. Example

a. Calibration

A 178.25 ft base line was laid out along a flat sidewalk.

A surveyor paced the base line multiple times and recorded these counts: 71.5, 74.0, 73.5, 74.5

All counts were to nearest half pace.

Accept the last three counts as they meet 1/50 precision.

Average pace = (74.0+73.5+74.5)/3 = 74.0 p

There are 3 sig fig in the average paces.

Wait a minute: according to the sig fig additive rule, the sum of the three pace counts is 222.0 which has 4 sig fig. Dividing by 3 (an exact number) would be 74.00 to 4 sig fig.

But we have to take into account the pace resolution. Since each measurement is only good to 1/2 pace, expressing the average to 0.01 pace based on only three samples doesn't make sense.

So 74.0 paces it is.

Conversion factor

The base line length has 5 sig fig.

Pace count

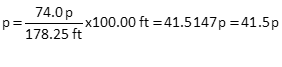
The pace count has 3 sig fig because of the average paces.

b. Unknown distance

She then paced an unknown distance multiple times with these counts: 93.5, 93.0, 94.0, 91.0

The first three counts meet the 1/50 criterion.

Average pace = (93.5+93.0+94.0)/3 = 93.5 p

This has 3 sig fig.

Distance using conversion factor

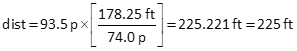
93.5 p and 74.0 p both have 3 sig fig, so the paced distance would also.

The distance is good to the nearest foot, which makes sense considering what it was measured with.

Distance using pace count

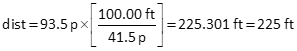
93.5 p and 41.5 p both have 3 sig fig, so the paced distance would also. Consider the 100.00 ft exact since the pace count is per 100 feet.