B. Pacing
1. Theory
The oldest form of distance measuring instrument is the human body. It's a convenient instrument because it's always available - you never forget to bring it along. Some units derived from the body include:
- Distance from end of middle finger of outstretched arm to nose is a yard.
- A hand is four inches
- The middle joint length of the little finger is an inch.
- The foot is, well, from a foot
Although handy, such measurements aren’t useful when you have long distances to measure.
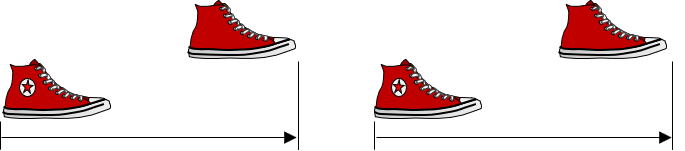
Another form of measurement using the body is pacing: basically controlled walking, Figure B-1.
|
|
| Figure B-1 Pacing |
Walking at a uniform steady rate means footfalls are generally equally spaced. With pacing, longer distances become easier to measure.
2. Principle
a. What's a "pace"?
Hard to believe, but we can take the simple action of walking and over-complicate it to measure distances.
The chapter title is Pacing, which is pretty generic. But what constitutes a pace? And does it differ from step or stride? Does it make a difference if we count it every time the left foot lands, or the right foot, or either foot?
To keep it simple, we will define pace as the unit measured each time either foot lands. That's pretty easy to remember and apply.
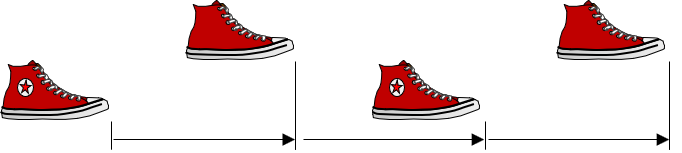
But wait, we still have an issue: our feet themselves have length, Where on our feet does a pace begin and end? Figure B-2 shows four different ways we can define a pace.
|
|
| (a) Heel-to-Toe |
|
|
| (b) Toe-to-Toe |
|
|
| (c) Heel-to-Heel |
|
|
| (d) Arch-to-Arch |
| Figure B-2 Pace |
Heel-to-Toe, Figure B-2(a), shouldn't be used because it has an undefined space between successive paces; the others are fine. Which to use is a matter of personal preference although Heel-to-Heel, Figure B-2(c), allows pacing to start at the base of a wall, Figure B-3.
|
|
| Figure B-3 Starting at a Wall |
b. Calibration
Most linear units (with a few notable exceptions) have fixed length regardless where applied, but not everyone's pace is the same length. Expressing a distance in paces (or area in square paces) is ambiguous and must be converted to some conventional unit others can understand. This requires a conversion factor, determined through a calibration process.
For reliable results, calibration should be performed under controlled conditions.
(1) Calibration conditions
Open flat base line path allowing uninterrupted pacing in both directions
Lay out a base line that is 100 to 300 feet long.
Establish base line length to a higher accuracy than pacing
Warm windless day
Shoes and clothes typically worn in surveying field situations
(2) Procedure
Base line should be paced at least three times and until at least a 1/50 precision is consistently achieved
Reasonable resolution is a half pace.
All pace counts are recorded, those outside the precision will be rejected for subsequent computations
Compute conversion factor and pace count.
Conversion factor is base line length over the average pace, Equation B-1.
Pace count is the number of paces per 100 feet (or 100 meters), Equation B-2.
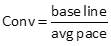 |
Equation B-1 |
 |
Equation B-2 |
(3) Application
For highest accuracy, pace the unknown distance enough times to achieve consistently.
Apply either the conversion factor or pace count to determine the unknown distance.
How accurately can a distance be determined by pacing? As we'll see in the Errors section, there are a number of things which can affect pacing. Remember that pacing resolution is about a half pace which for most people is between 1 and 1.5 feet. Obviously that resolution does not support distance determination to a hundredth of a foot. It's best to use the rules of significant figures to express a paced distance to a reasonable level of accuracy.
3. Example
a. Calibration
A 178.25 ft base line was laid out along a flat sidewalk.
A surveyor paced the base line multiple times and recorded these counts: 71.5, 74.0, 73.5, 74.5
All counts were to nearest half pace.
Accept the last three counts as they meet 1/50 precision.
Average pace = (74.0+73.5+74.5)/3 = 74.0 p
There are 3 sig fig in the average paces.
Wait a minute: according to the sig fig additive rule, the sum of the three pace counts is 222.0 which has 4 sig fig. Dividing by 3 (an exact number) would be 74.00 to 4 sig fig.
But we have to take into account the pace resolution. Since each measurement is only good to 1/2 pace, expressing the average to 0.01 pace based on only three samples doesn't make sense.
So 74.0 paces it is.
Conversion factor
![]()
The base line length has 5 sig fig.
Pace count
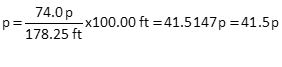
The pace count has 3 sig fig because of the average paces.
b. Unknown distance
She then paced an unknown distance multiple times with these counts: 93.5, 93.0, 94.0, 91.0
The first three counts meet the 1/50 criterion.
Average pace = (93.5+93.0+94.0)/3 = 93.5 p
This has 3 sig fig.
Distance using conversion factor
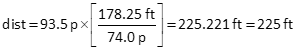
93.5 p and 74.0 p both have 3 sig fig, so the paced distance would also.
The distance is good to the nearest foot, which makes sense considering what it was measured with.
Distance using pace count
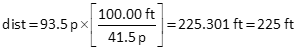
93.5 p and 41.5 p both have 3 sig fig, so the paced distance would also. Consider the 100.00 ft exact since the pace count is per 100 feet.
4. Error Sources and Behavior
a. Instrumental / Personal
(1) Consistency
(a) Principle
It may take some time for a new surveyor to settle into a comfortable, consistent walking rate.
(b) Behavior
Random
(c) Compensation
Practice and paying attention to other errors
(2) Footgear
(a) Principle
Shoe type, Figure B-4, affects how a person walks.
   |
| Figure B-4 Footgear |
(b) Behavior
Random.
(c) Compensation
Use footgear typically worn in field situations.
(3) Counting
(a) Principle
Forgetting the count as you are pacing can happen, particularly on longer distances.
(b) Behavior
Mistake.
(c) Compensation
Repeat measurements to find and discard mistaken counts.
(4) Individual v Group
(a) Principle
Everyone has their own normal stride. When walking in a group, some individuals speed up, others slow down so the group stays together. This happens subconsciously and will affect pacing.
(b) Behavior
Random.
(c) Compensation
Walk alone.
(5) Self-consciousness
(a) Principle
The key to successful pacing is to maintain a normal comfortable walking rate. Doing something out of the ordinary will affect pacing.
Step off normally when stating a pace (many first-timers exaggerate the initial step).
Don't look down at your feet (you won't leave them behind), instead watch where you're going and to see obstacles.
Use peripheral vision at the end of the pace to avoid stretching or shrinking the last step.
Believe it or not, some people still remember and react to "Step on a crack, break your mother's back." (If you didn't before, you will now as I've planted the seed)
(b) Behavior
Random.
(c) Compensation
Practice.
(6) Computations
(b) Principle and Behavior
Over/understating accuracy, math blunder, etc. Mistake.
(c) Compensation
Care and review.
b. Natural
(1) Terrain
(a) Principle
In Surveying we use horizontal distances; pacing returns a distance along the ground, Figure B-5. On rolling terrain, the paced distance will be too long.
 |
| Figure B-5 Pacing Along the Ground |
(b) Behavior
Random.
(c) Compensation
The only way to compensate is to make an adjustment based on terrain analysis.
(2) Slopes
(a) Principle
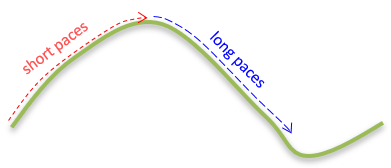
Slopes affect walking rate. Going uphill tends to shorten paces, downhill lengthens, Figure B-6.
|
|
| Figure B-6 Slope Effects |
(b) Behavior
Systematic/Random.
(c) Compensation
The only way to compensate is to make an adjustment based on terrain analysis.
(3) Temperature
(a) Principle
We tend to walk more quickly in cold weather than warm which affects pace lengths.
(b) Behavior
Random.
(c) Compensation
Re-calibrate under cold conditions.