G. Horizontal Angles
1. Definition
A horizontal angle is measured perpendicular to gravity. Three points are involved:
-
Backsight (BS)
-
Foresight; FS
-
At
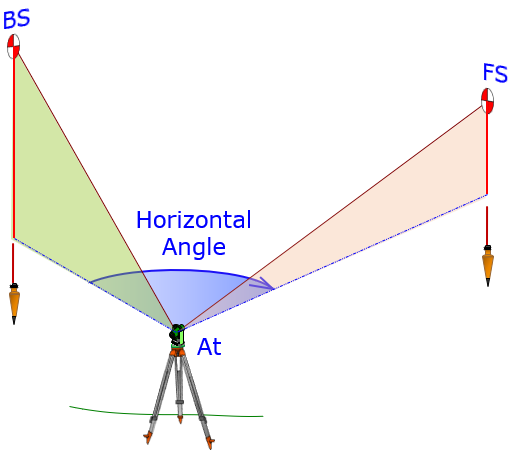
The angle is between two vertical planes; one contains the BS and At points, the other contains the FS and At. The At point is generally occupied by a surveying instrument, Figure G-1.
|
|
|
Figure G-1 |
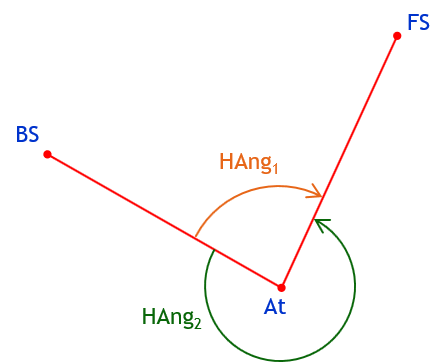
If we look down on the horizontal plane with the three points, Figure G-2, we see there are two horizontal angles between the vertical planes: HAng1 and HAng2.
|
|
|
Figure G-2 |
This causes an ambiguous situation unless we can specifically identify which angle we mean. Recall that the four parts of an angle are:
-
Start
-
Direction
-
Magnitude
-
End
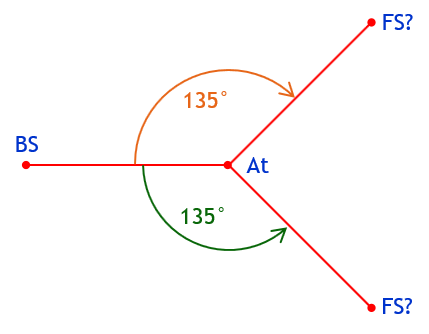
HAng1 and HAng2 have the same start (BS) and end (FS) but different direction and magnitude. All four parts must be clearly defined. Merely including magnitude without a direction doesn’t resolve the ambiguity. For example, a 135° angle from BS to FS could still be interpreted two ways, Figure G-3.
|
|
|
Figure G-3 |
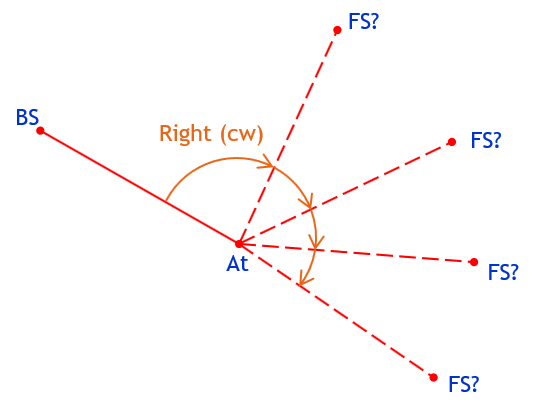
Similarly, expressing a direction, to the right (clockwise) or left (counterclockwise), without a magnitude is also unclear, Figure G-4.
|
|
|
Figure G-4 |
There are a few different ways to specify horizontal angles which help minimize confusing interpretations.
2. Types of Horizontal Angles
a. Interior/Exterior
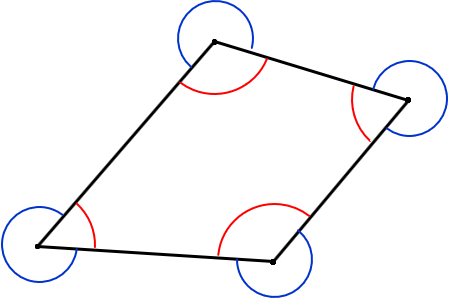
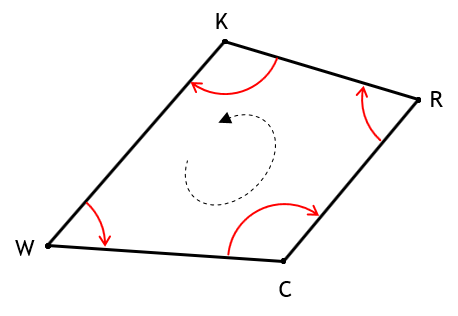
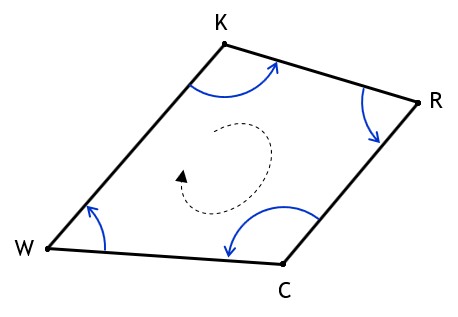
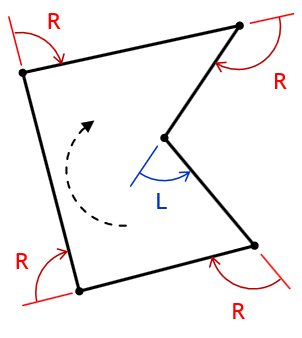
On a closed non-crossing polygon, Figure G-5, horizontal angles can be either interior (red) or exterior (blue).
|
|
|
Figure G-5 |
The geometric condition for a non-crossing polygon is Equation (G-1).
|
|
Equation (G-1) |
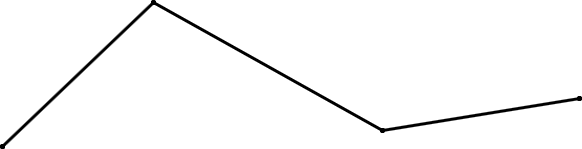
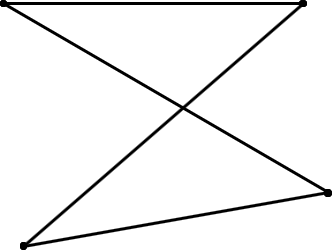
Interior and exterior don’t make sense if the polygon is open, Figure G-6(a), or if the polygon crosses itself, Figure G-6(b).
|
|
|
a. Open Polygon |
|
|
|
b. Crossing Polygon |
|
Figure G-6 |
In the latter case, the polygon turns itself inside-out and Equation (E-1) does not apply. Open and crossing polygons need some other way to express an angle.
b. Right/Left
Right or left is the rotational direction from the BS point to the FS point. Consider standing on the At point, looking at the BS point: an angle to the right means you physically turn your body to the right to see the FS point. An angle right is clockwise, left counter-clockwise, Figure G-7.
|
|
|
Figure G-7 |
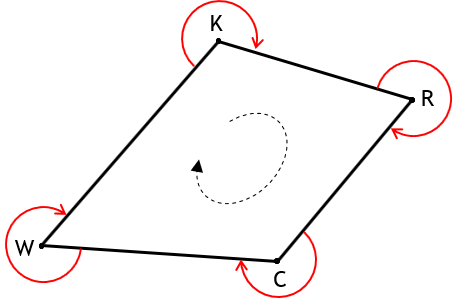
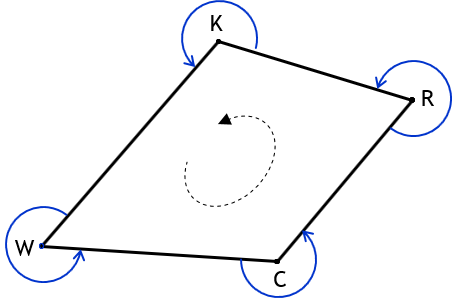
Figure G-8(a) shows a closed non-crossing polygon with interior angles to the right; Figure G-8(b) to the left.
|
|
|
a. Angles Right |
|
|
|
b. Angles Left |
|
Figure G-8 |
The dashed lines in Figure G-8 show the angle measurement sequence. In Figure G-8(a), interior angles to the right measurement progresses counter-clockwise around the polygon.
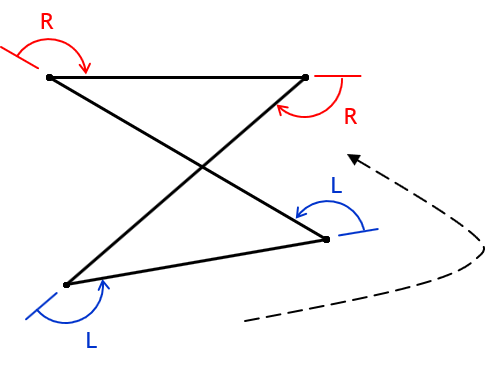
We can also have exterior angles to the right, Figure G-9(a), and to the left, Figure G-9(b).
|
|
|
a. Angles Right |
|
|
|
b. Angles Left |
|
Figure G-9 |
Right or left help with angle definitions on the open and crossing polygons. In Figure G-10, progressing in the direction of the dashed line, the open polygon has angles to the right.
|
|
|
Figure G-10 |
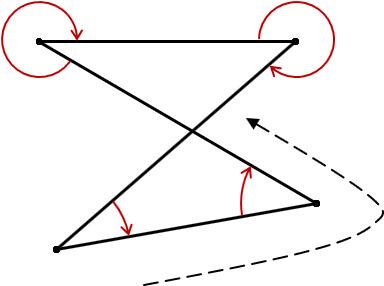
Figure G-11 shows a crossing polygon using angles left progressing in the direction of the dashed line.
|
|
|
Figure G-11 |
Note how the angles change from “interior” to “exterior” although there is no consistent polygon interior.
c. Deflection Angles
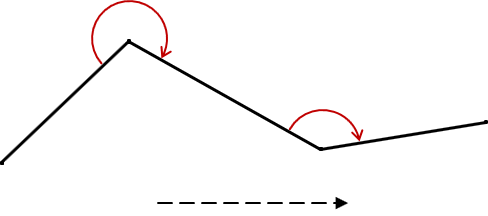
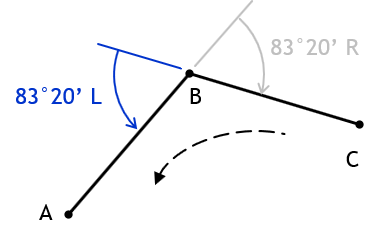
A deflection angle is how much the next line deflects from an extension of the previous line. It consists of two parts: (1) magnitude and (2) direction. For example, in Figure G-12:
Line BC deflects from line AB 45° to the right, written as 45°R.
Line CD deflects from line BC 30°L.
|
|
|
Figure G-12 |
A deflection angle ranges from 0° (no deflection) to 180° (going back along the preceding line).
The mathematical angle condition for a closed non-crossing polygon, Figure G-13, is:
|
|
Equation (G-2) |
Right deflection angles are positive (+), left are negative (-).
|
|
|
Figure G-13 |
Equation (G-2) is also the mathematical condition for a closed polygon which crosses itself an even number of times. For an odd number of crossings, Figure G-14, the mathematical condition is:
|
|
Equation (G-3) |
|
|
|
Figure G-14 |
How does reversing travel direction around a polygon change the deflection angles? Figure G-15 shows that the deflection angle value is the same, but its direction is reversed.
|
|
|
|
a. Clockwise Travel |
b. Counterclockwise Travel |
|
Figure G-15 |
|
3. Example Problem
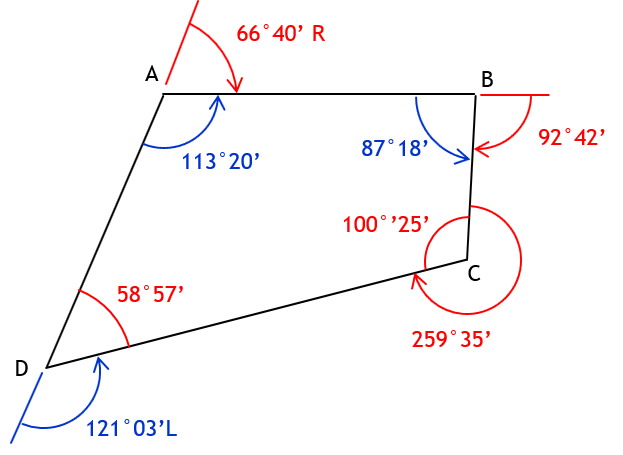
Given this polygon with combination of angle types:
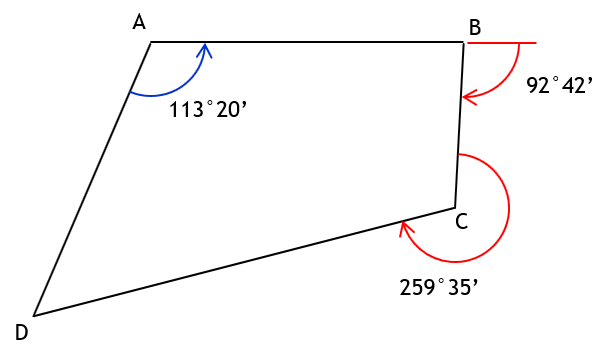
Determine
a. Deflection angle at A from D to B
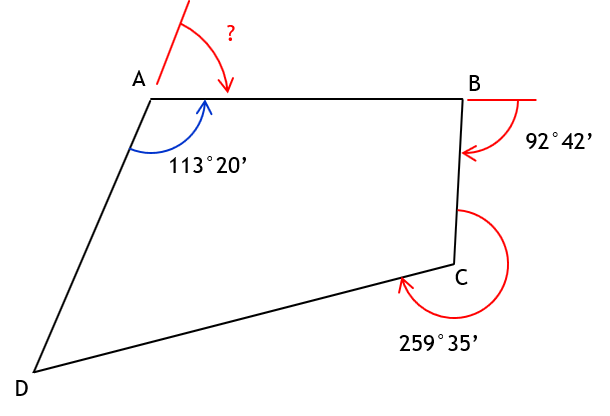
Defl angle A = 180°00’ - 113°20’ = 66°40’ = 66°40’ R
b. Angle left at B from A to C
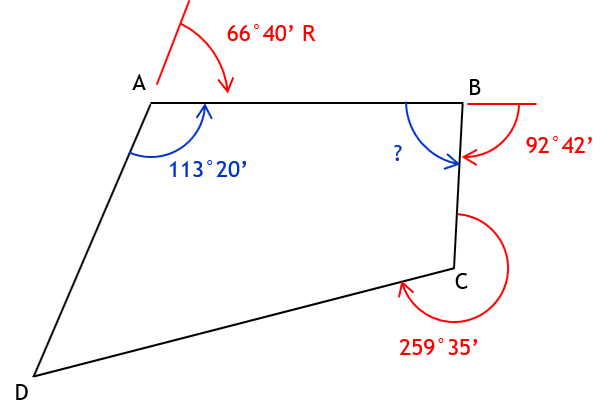
Int angle B = 180°00’ - 92°42’ = 87°18’
c. Deflection angle at D from A to C
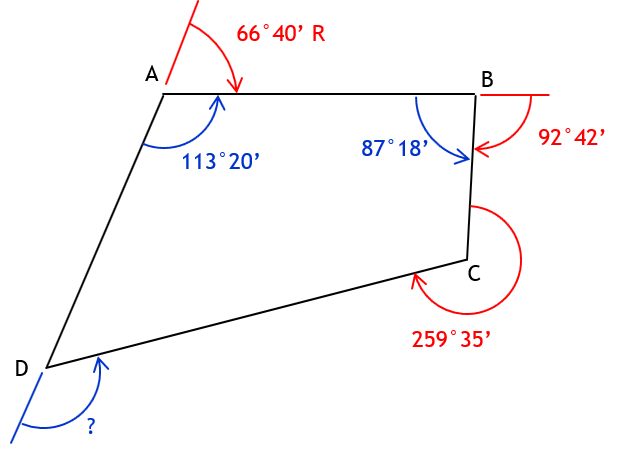
Need interior angle at D to compute the deflection angle.
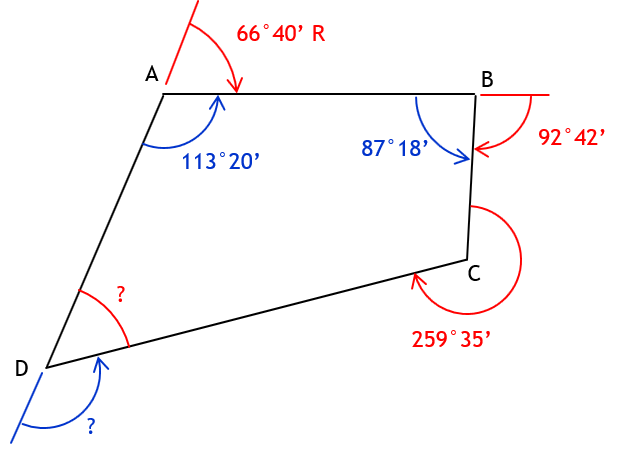
To compute interior angle at D, subtract the sum of the other interior angles from (n-2)x180°.
Need interior angle at C.
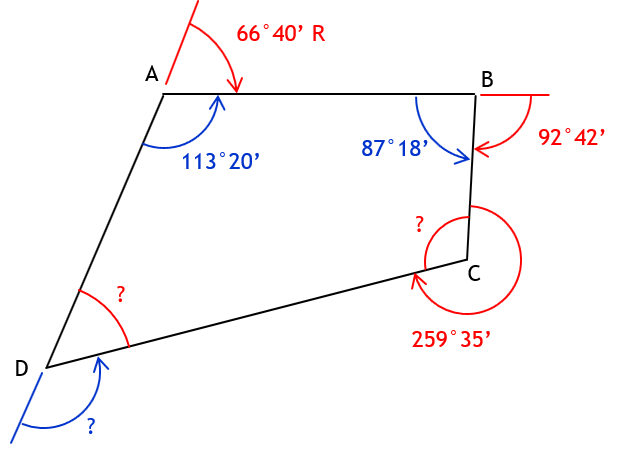
Int angle C = 360°00’ - 259°35’ = 100°25’
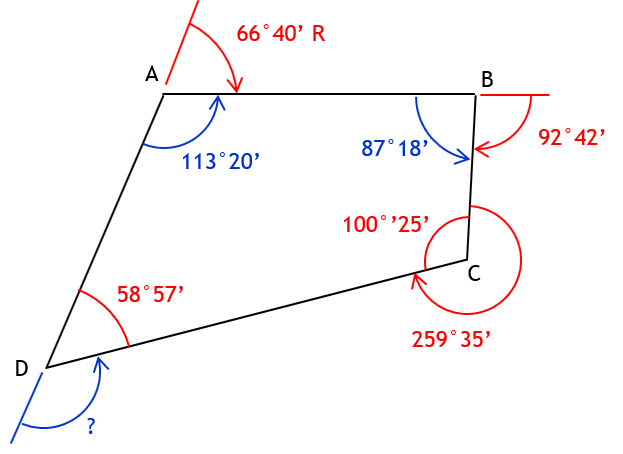
Int angle D = (4-2)x180°00’ - (113°20’ + 87°18’ + 100°25’) = 360°00’ - 301°03’ = 58°57’

Defl angle D = 180°00’ - 58°57 = 121°03’ = 120°03’ L