2. Vertical and Zenith Conversions
Converting between vertical and zenith angles is pretty simple as long as one thing is remembered: A vertical angle is ambiguous while a zenith angle is not.
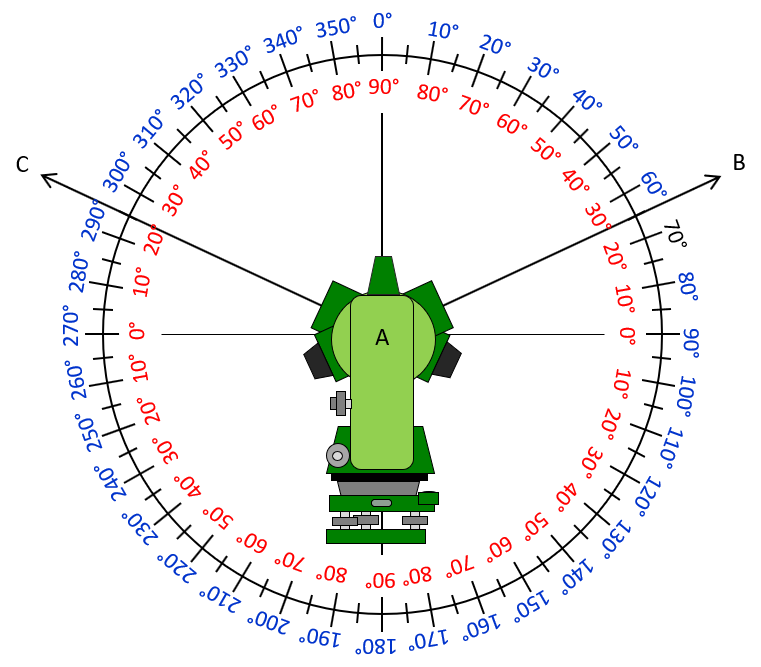
What does that mean? In Figure F-5, lines AB and AC both have a +25° vertical angle but different zenith angles of 65° and 295°, respectively.
|
|
|
Figure F-5 |
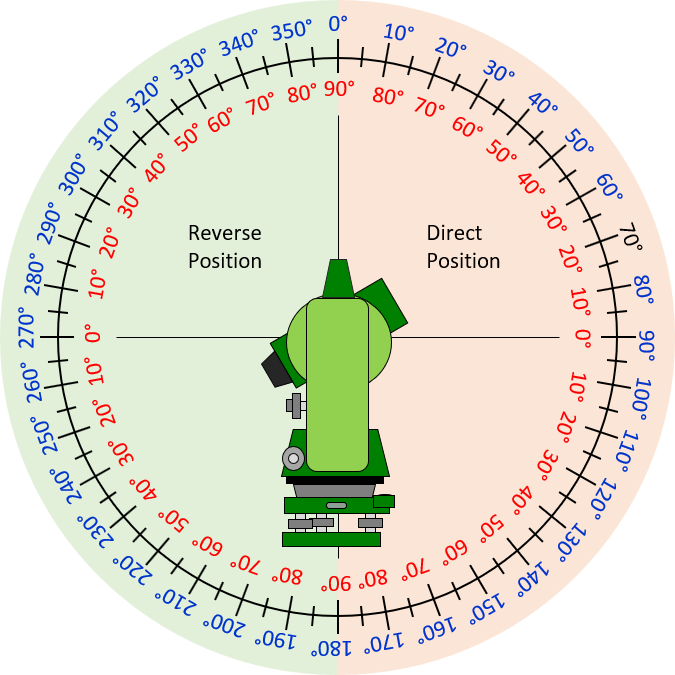
To convert from a vertical angle to zenith requires knowing which side of the zenith circle is involved. Traditionally, the 0°-90°-180° side of the circle is an instrument’s direct position while the 180°-270°-0° side is the reverse position, Figure F-6 (more on that in the later angle measurement topics).
|
|
|
Figure F-6 |
An analog instrument (transit or theodolite) uses only one type of vertical circle. Converting between vertical and zenith angles is only necessary if subsequent calculations require one form or the other.
On modern digital instruments with electronically encoded circles rather than physically divided ones, either type of angle measurement can be used. It’s a matter of software.
But to show the relationship between the two, we will perform a few example conversions.
Example 1
Convert a 56°40’ zenith angle to a vertical angle.
As with most surveying problems, a sketch helps visualize the problem:
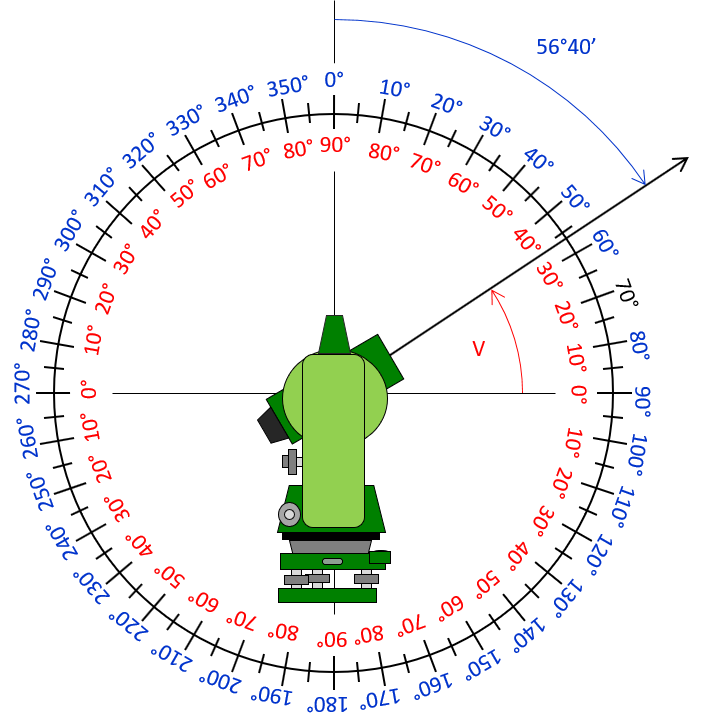
Because it is above horizontal, the vertical angle is positive.
Example 2
Convert a 227°30’ zenith angle to a vertical angle.
Sketch:
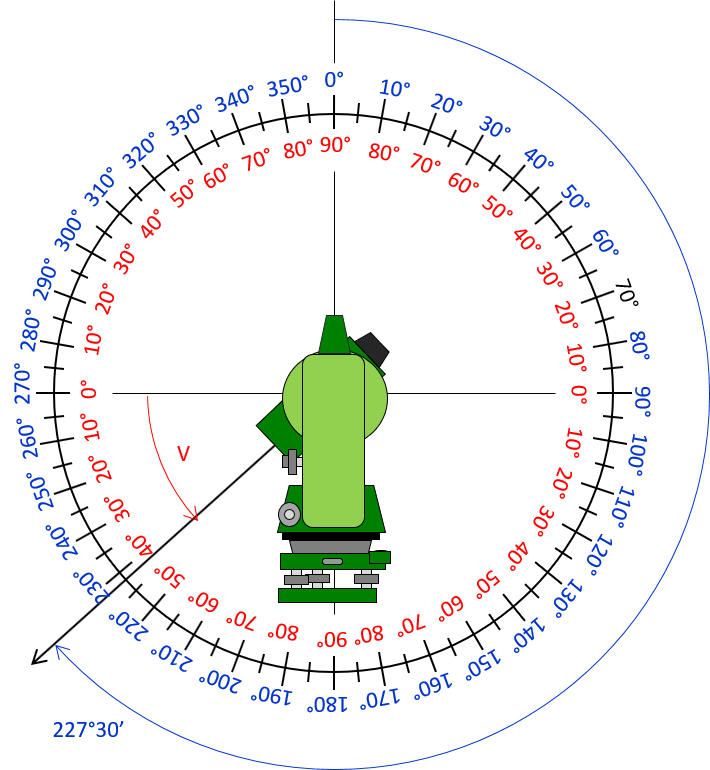
Because it is below horizontal, the vertical angle is negative.
Example 3
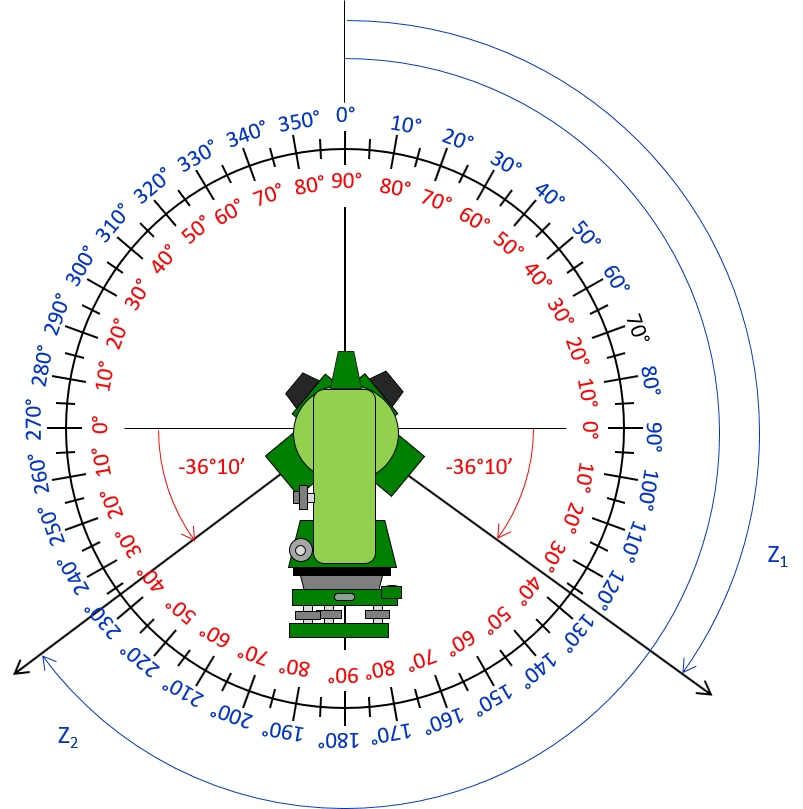
Which zenith angles are the same as a -36°10’ vertical angle?
Recall that there are two vertical angles one on each side of the zenith circle.
Sketch: