F. Vertical Angles
1. Definition; Types
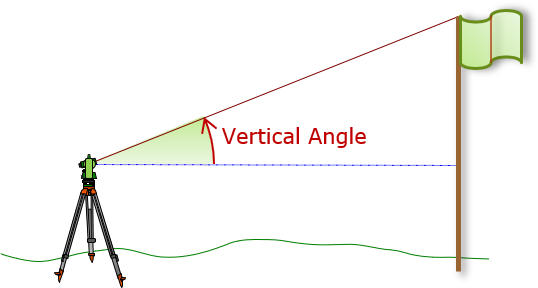
A vertical angle is measured in the direction of gravity, Figure F-1
|
|
|
Figure F-1 |
There are two types:
- Traditional Vertical (or just Vertical)
- Zenith
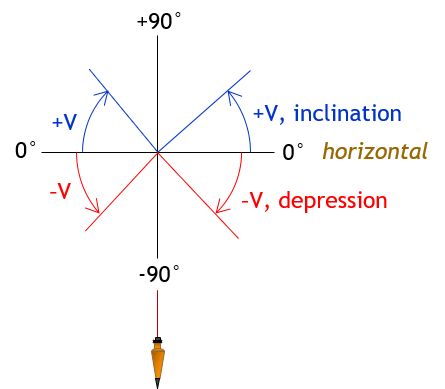
A traditional Vertical angle is measured up or down from horizontal, Figure F-2. It ranges from -90° below horizontal (depression) to +90° above (inclination). This is typical of angle measurements with traditional open-standards American transits.
|
|
|
Figure F-2 |
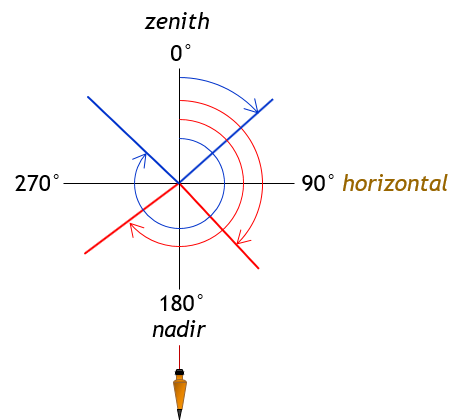
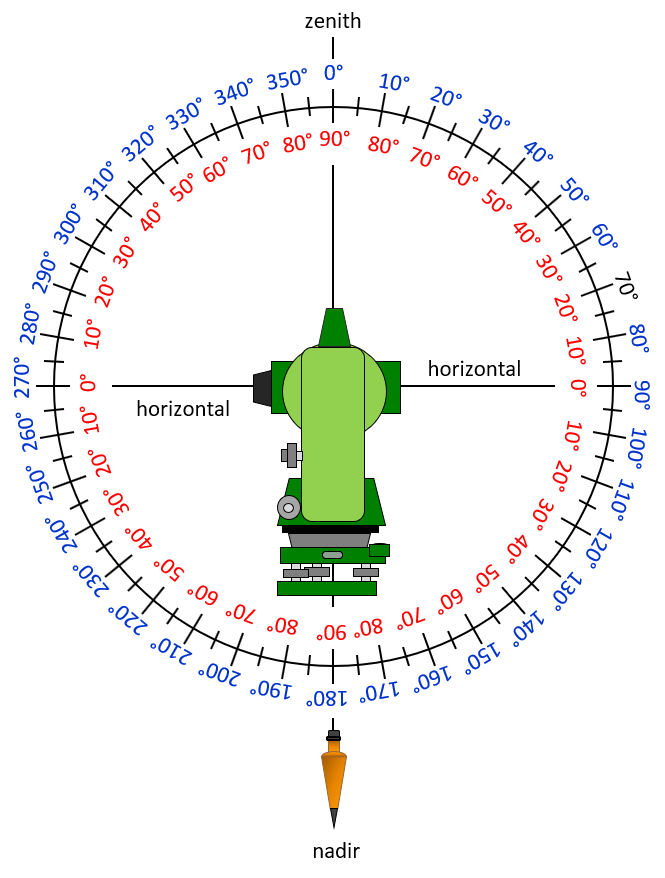
A Zenith angle is measured from the upper end of the vertical line continuously all the way around, Figure F-3. It ranges from 0° directly upward (zenith) to 90° on the horizontal to 180° directly downward (nadir) to 270° on the opposite horizontal to 360° back at the zenith. This is typical of angle measurements with closed-standards optical transits and theodolites.
|
|
|
Figure F-3 |
Figure F-4 shows combined Vertical (red) and Zenith (blue) angle circles with an instrument at their center as a reference. This figure helps understand how the two types of angles relate to each other.
|
|
|
Figure F-4 |
2. Vertical and Zenith Conversions
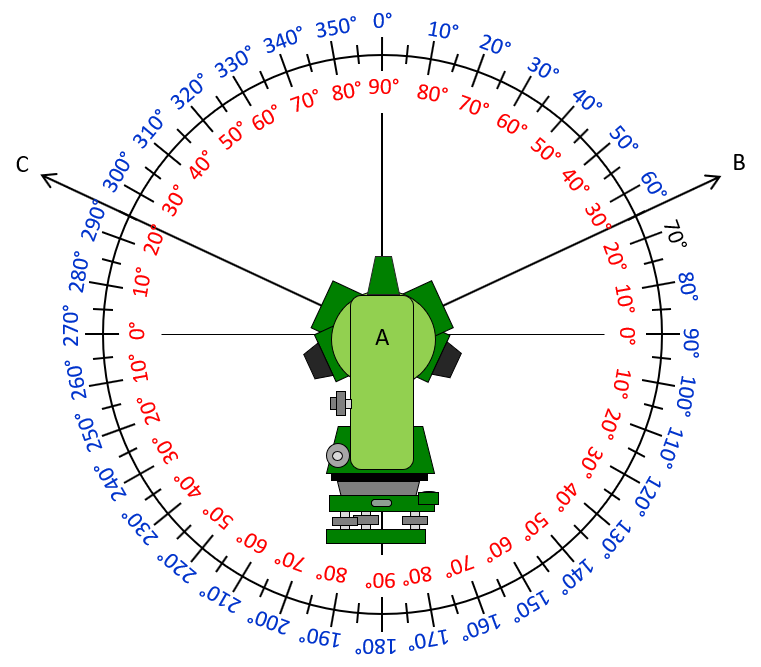
Converting between vertical and zenith angles is pretty simple as long as one thing is remembered: A vertical angle is ambiguous while a zenith angle is not.
What does that mean? In Figure F-5, lines AB and AC both have a +25° vertical angle but different zenith angles of 65° and 295°, respectively.
|
|
|
Figure F-5 |
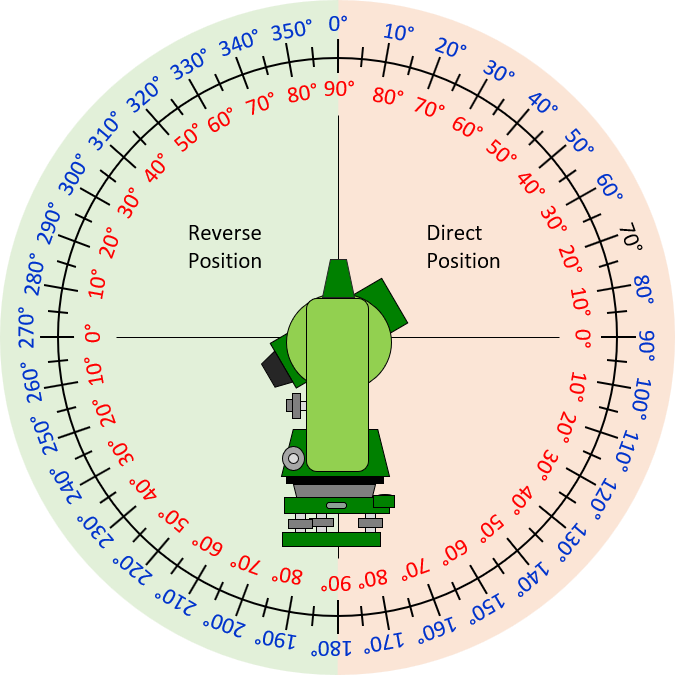
To convert from a vertical angle to zenith requires knowing which side of the zenith circle is involved. Traditionally, the 0°-90°-180° side of the circle is an instrument’s direct position while the 180°-270°-0° side is the reverse position, Figure F-6 (more on that in the later angle measurement topics).
|
|
|
Figure F-6 |
An analog instrument (transit or theodolite) uses only one type of vertical circle. Converting between vertical and zenith angles is only necessary if subsequent calculations require one form or the other.
On modern digital instruments with electronically encoded circles rather than physically divided ones, either type of angle measurement can be used. It’s a matter of software.
But to show the relationship between the two, we will perform a few example conversions.
Example 1
Convert a 56°40’ zenith angle to a vertical angle.
As with most surveying problems, a sketch helps visualize the problem:
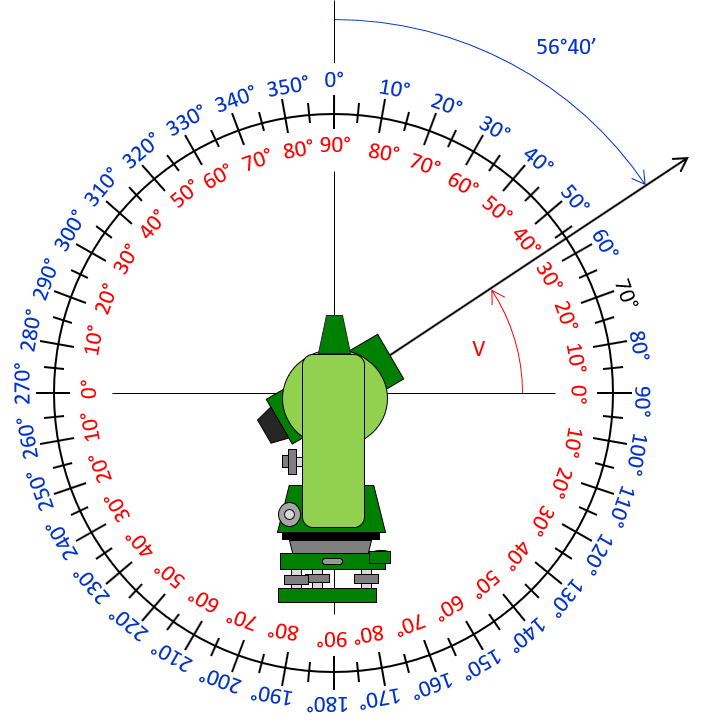
Because it is above horizontal, the vertical angle is positive.
Example 2
Convert a 227°30’ zenith angle to a vertical angle.
Sketch:
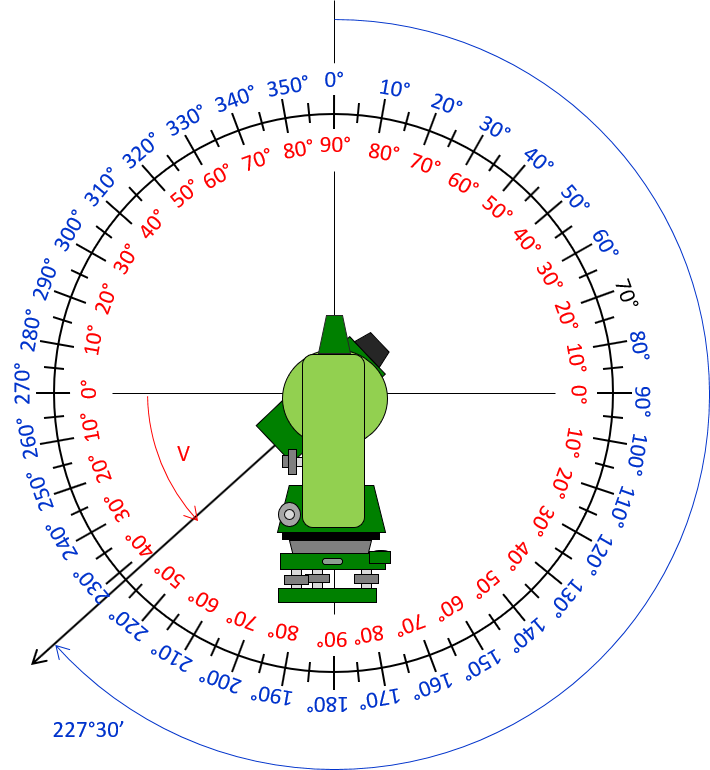
Because it is below horizontal, the vertical angle is negative.
Example 3
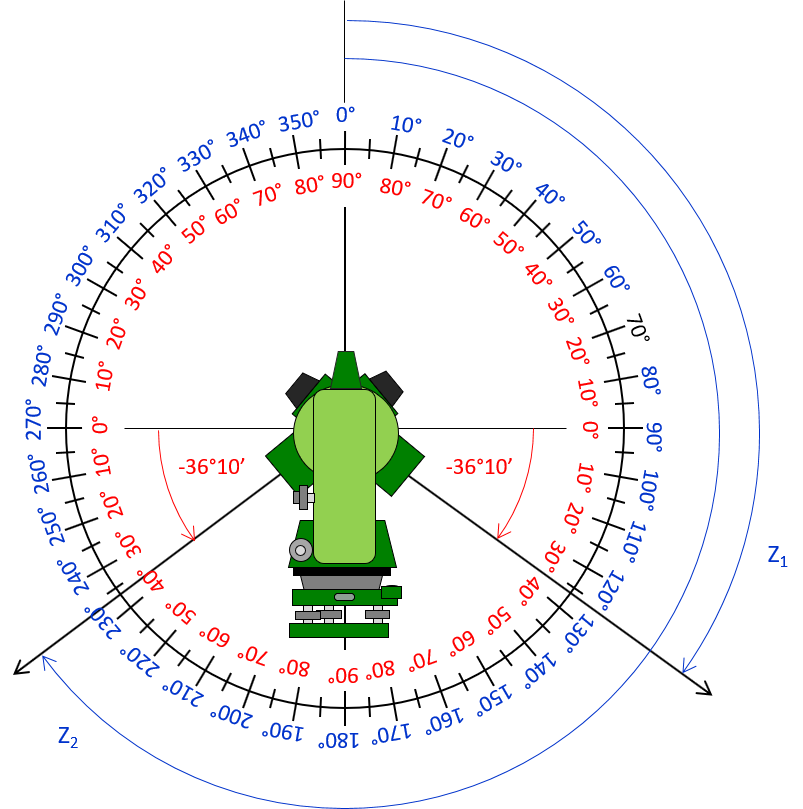
Which zenith angles are the same as a -36°10’ vertical angle?
Recall that there are two vertical angles one on each side of the zenith circle.
Sketch: