3. Reverse curve
a. General
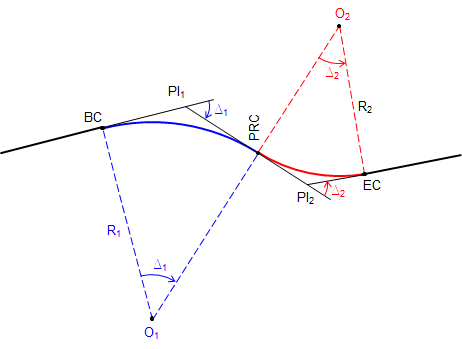
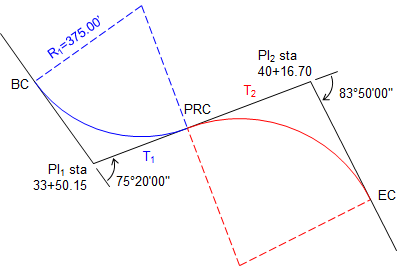
A reverse curve consists of two consecutive tangent curves with radius points on opposite sides of the center line. Figure 15 shows basic nomenclature and parts.
 |
| Figure D-15 Nomenclature |
The PRC is the Point of Reverse Curvature, and is the EC of the first curve and BC of the second.
The distance from PI1 to PI2 is T1 + T2. Because of this relationship, as soon as one curve's geometry is fixed, so is the other's. This makes a reverse curve generally easier to compute than a compound curve.
Once the geometry of both curves are fixed, they can be computed as individual simple curves.
b. Stationing
Stationing can be a little confusing since there can be a station equation at both the PRC and EC of the second curve. Usually, if a stationing is maintained along the tangents, then a station equation only appears at the end of the reverse curve.
To compute stationing:
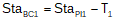 |
Equation D-6 | |
 |
Equation D-7 | |
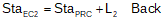 |
Equation D-8 | |
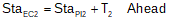 |
Equation D-9 |
b. Example
For a reverse curve, the first PI is at 33+50.15 with a 75°20'00"L deflection angle and second PI is at 40+16.70 with a 83°50'00"R deflection angle.
The first curve has a 375.00' radius. Determine the radius of the second curve.
Sketch:
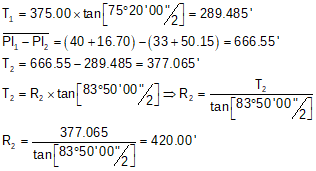
Ta-daa!