Solution: Trig Leveling
Problem (1)
A TSI is set up 5.41' over point Q whose elevation is 745.39'. The following readings are taken:
| Point | Horizontal angle |
Vertical angle |
Slope distance |
| 101 | 0°00'00" | 4°24'10" | 145.25' |
| 102 | 39°56'15" | -6°00'25" | 89.32' |
| 103 | 79°05'45" | -2°58'30" | 118.95' |
The reflector height in each case was 5.64'. The instrument and reflector heights were measured with the same cloth tape.
What are the horizontal distances to and elevations of the observed points? Compute values to 0.01'.
Solution
To use the equations from Chapter D. Stadia, each vertical angle must be converted to a zenith angle.
Point 101
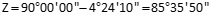
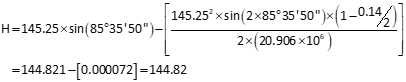
Because the curvature and refraction is so small, it can be ignored for the other horizontal distances.
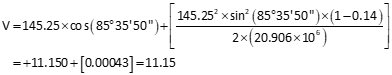
Because the curvature and refraction is so small, it can be ignored for the other vertical distances.
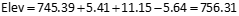
Point 102

Point 103
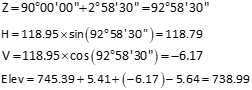
Solution
| Point | Horiz dist | Elevation |
| 101 | 144.82 | 756.31 |
| 102 | 88.83 | 735.81 |
| 103 | 118.79 | 738.99 |
Problem (2)
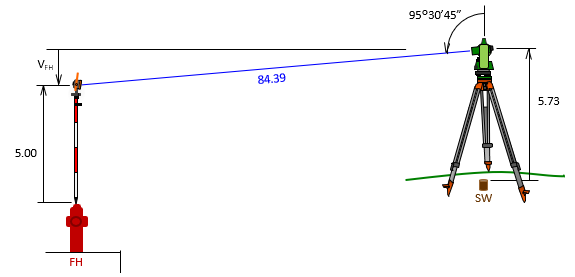
A TSI is set up over the SW corner of a property. The TSI height is 5.73' above the corner, measured with a fiberglass tape. The elevation of the top nut on a fire hydrant (FH) across the street is 827.43'.
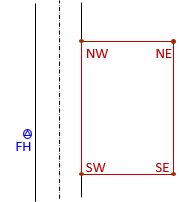
From the TSI, the following readings are taken
| Point | Reflector Height1 |
Slope distance |
Horizontal angle |
Zenith angle |
| FH | 5.00 | 84.39' | 0°00'00" | 95°30'45" |
| NW | 6.25 | 194.48' | 44°51'55" | 87°05'35" |
| NE | 6.25 | 240.68' | 80°56'30" | 85°48'05" |
| SE | 7.50 | 142.02' | 134°51'35" | 92°23'50" |
1Measured with the same fiberglass tape.
What are the elevations of the four property corners? Compute to 0.01' to minimize rounding error.
Solution
We saw in the previous problem that over short distances, curvature and refraction are too small to affect elevations.
Point SW
Determine the elevation of the TSI at point SW from the fire hydrant, then the elevation of point SW from the TSI.
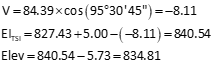
Point NW
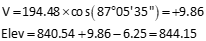
Point NE
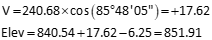
Point SE
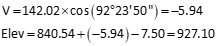
Solution
| Point | Elev |
| NW | 844.15 |
| NE | 851.91 |
| SE | 927.10 |