2. Bearings From Interior Angles
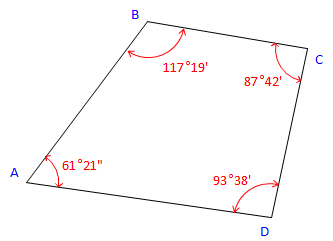
Given the following traverse and horizontal angles:
|
|
|
Figure C-23 |
Using a bearing of N 36°55' E for line AB, determine the bearings of the remaining lines clockwise around the traverse.
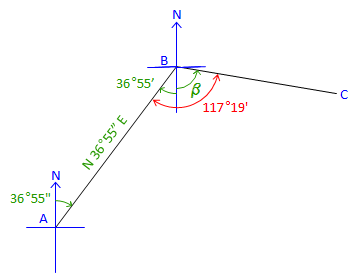
| At point B: | |
|
Figure C-24 |
Label the bearing angle, 36°55', from B to A. Subtract it from 117°19'. β = 117°19' - 36°55' = 80°24'Brg BC = S 80°24' E |
|
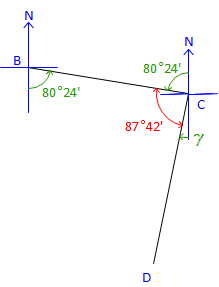
At point C: |
|
|
Figure C-25 |
Label the bearing angle, 80°24', from C to B. Subtract it along with 87°42' from 180°00' to get bearing angle CD. γ = 180°00' - (80°24' + 87°42') = 11°54' Brg CD = S 11°54' W |
|
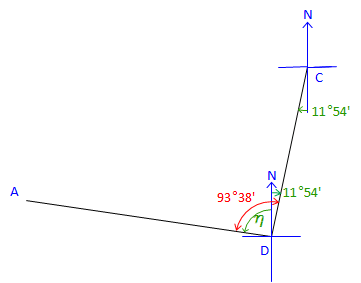
At point D: |
|
|
Figure C-26 |
Label the bearing angle, 11°54', from D to C. Subtract it from 93°38' to obtain next bearing angle. &eta= 93°38' - 11°54' = 81°44'Brg DA = N 81°44' W |
|
The directions for all four traverse lines have been computed. Angles at B, C, and D have been used, but that at A has not. For a math check, use the Bearing of DA and the angle at A to compute the bearing we started with. |
|
|
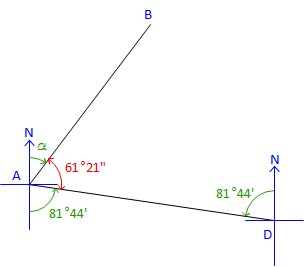
Figure C-27 |
Label the bearing angle, 81°44', from A to D. Subtract it along with 61°21' from 180°00' to get next bearing angle. α = 180°00' - (61°21' + 81°44') = 36°55 Brg AB = N 36°55' E check |
If our computed and initial bearings for AB don’t match it means one of two things:
- there is a math error in our computations, or,
- the interior angles weren’t balanced.
On this traverse the angles sum to 360°00' so there is no angular misclosure. If our math check had failed it would have been due to a math error in our computations.
Had the angles not been balanced and if there were no math errors, the math check would be off by the angular misclosure.
Summary:
| Line | Bearing |
| AB | N 36°55' E |
| BC | S 80°24' E |
| CD | S 11°54' W |
| DA | N 81°44' W |