I. Traverse Adjustment by Coordinates
1. Coordinates Galore
Most software compute and carry coordinates through each step of the traverse computations. Until final traverse adjustment, the coordinates go thru a series of values. For example, in a traditional non-least squares approach coordinates would be computed:
- From raw measurements and directions using unadjusted angles, then,
- After angles are adjusted, and,
- After the traverse is adjusted - these are the final coordinate values.
While coordinates are not needed for manual computations, they can be included. If so they are usually computed after angles are balanced: we will refer to these as preliminary coordinates.
2. Adjustment Process
The traverse misclosure is determined by comparing the preliminary coordinates of the end point to its known starting coordinates:
Loop traverse, Figure I-1:
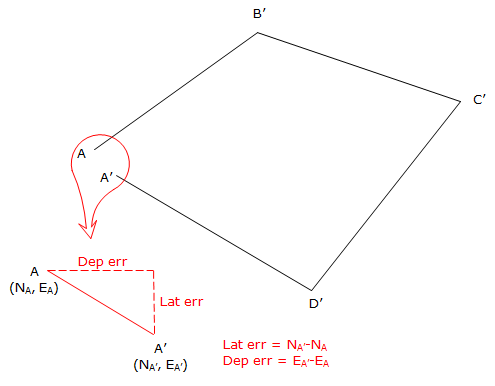 |
|
Figure I-1 |
On a loop traverse, the coordinates of the first point can be known or assumed.
Link traverse, Figure I-2.
The coordinates of the traverse endpoints must be known in the same system.
In this case E and H are known.
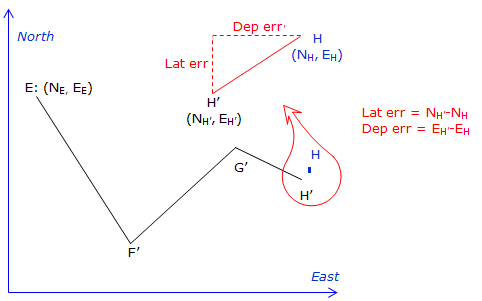 |
|
Figure I-2 |
When the traverse is adjusted, corrections are applied directly to the preliminary coordinates (J') to obtain final coordinates (J), Figure I-3 and Equations E-3 and E-4.
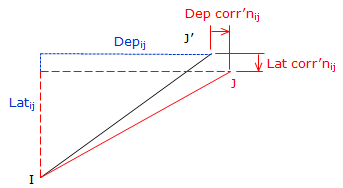 |
|
Figure I-3 |
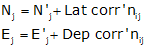 |
Equations E-3 and E-4 |
The line correction affects the line's endpoint, that is, the position of J changes relative to the position of I by the latitude and departure corrections of the line IJ.
Because the coordinates of J change, the coordinates of the next point, K, must change by the same amount plus the correction of the line JK, Figure I-4:
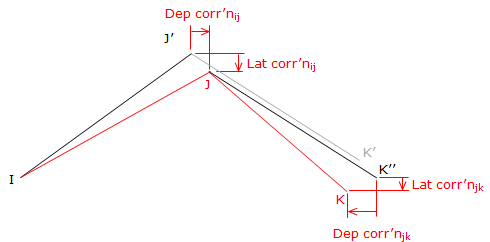 |
|
Figure I-4 |
The position shift from K' to K'' is the same as the shifts from J' to J.
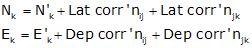
This pattern of accumulating corrections continues until the final point where the adjusted coordinates should equal the known values.
Using the Compass Rule:
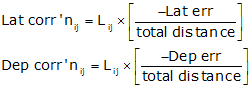 |
Equations E-1 and E-2 |
To compute coordinate corrections, the equations are modified to:
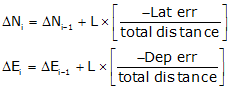 |
Equations I-1 and I-2 |
where ΔNi-1 and ΔEi-1 in each are the cumulative previous corrections.
3. Examples
The traverse examples here are the same ones used as previous computation examples so we can check these against earlier results.
a. Loop Traverse
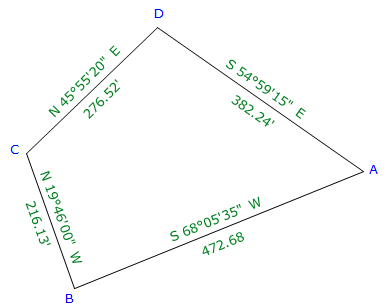 |
|
Figure I-5 |
Previously computed unadjusted latitudes and departures are:
| Line | Bearing | Length (ft) | Lat (ft) | Dep (ft) |
| AB | S 68°05'35"W | 472.68 | -176.357 | -438.548 |
| BC | N 19°46'00"W | 216.13 | +203.395 | -73.093 |
| CD | N 45°55'20"E | 276.52 | +192.357 | +198.651 |
| DA | S 54°59'15"E | 382.24 | -219.312 | +313.065 |
|
sum: |
1347.57 | +0.083 | +0.075 |
(1) Compute preliminary coordinates from the raw latitudes and departures:
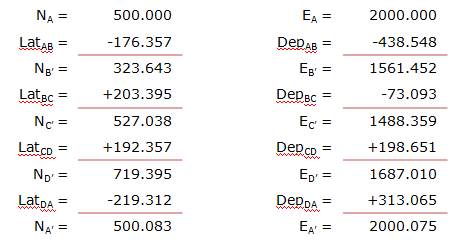
(2) Determine latitude and departure closure errors:
Lat err = NA' - NA = 500.083' - 500.000' = +0.083'
Dep err = EA' - EA = 2000.075' - 2000.000' = +0.075'
Note that these match the latitude and departure column sums above.
(3) Compute and apply corrections to the coordinates using the Compass Rule, Equation (I-3).
Line AB
Because point A is a control point, its coordinates are not modified. The corrections are applied to the line's endpoint, point B.
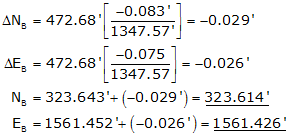
Line BC
Remember to include the corrections for the previous line.
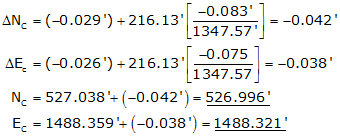
Line CD
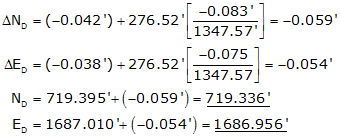
Line DA
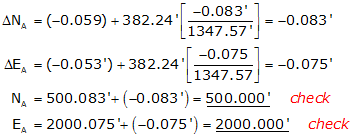
The corrected preliminary coordinates match the beginning coordinates of point A.
These coordinates also match those computed in the Coordinates section.
b. Link Traverse
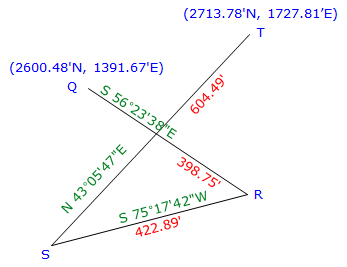 |
|
Figure I-6 |
Previously computed unadjusted latitudes and departures are:
|
Line |
Direction |
Length |
Lat |
Dep |
|
QR |
S 56°23'38"E |
398.75' |
-220.700' |
+332.104' |
|
RS |
S 75°17'42"W |
422.89' |
-107.347' |
-409.038 |
|
ST |
N 43°05'47"E |
604.49' |
+441.402' |
+413.004' |
|
|
sums: |
1426.13' |
+113.355' |
+336.070 |
(1) Compute preliminary coordinates:
|
Point |
North (ft) |
East (ft) |
|
|
Q |
2600.480 |
1391.670 |
|
|
LatQR |
-220.700 |
DepQR |
+332.104 |
|
R |
2379.780 |
|
1723.774 |
|
LatRS |
-107.347 |
DepRS |
-409.038 |
|
S |
2272.433 |
|
1314.736 |
|
LatST |
+441.402 |
DepST |
+413.004 |
|
T |
2713.835 |
|
1727.740 |
Lat err = 2713.835' - 2713.780' = +0.555'
Dep err = 1727.740'-1727.810' = -0.070'
(2) Compute and apply corrections to the coordinates using the Compass Rule, Equation I-3.
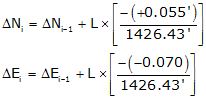
Computations for each line are not shown, but their results are tabulated below.
|
Point |
N' (ft) |
ΔN (ft) |
N (ft) |
E' (ft) |
ΔE (ft) |
E (ft) |
|
S |
2379.780 |
-0.015 |
2379.765 |
1723.774 |
+0.020 |
1723.794 |
|
T |
2272.433 |
-0.031 |
2272.402 |
1314.736 |
+0.041 |
1314.777 |
|
Q |
2713.835 |
-0.054 |
2713.781 |
1727.740 |
+0.071 |
1727.811 |
|
check |
check |