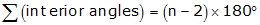B. Balancing Angles
1. Angle Condition
a.Interior Angles
For a closed non-crossing loop traverse, the angle condition is:
 |
Equation B-1 |
|
| Figure B-1 Angle Condtion - Loop |
||
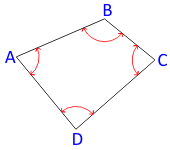
| A loop traverse which crosses itself doesn’t have conventional “interior” angles so Equation B-1 won’t work. Some other angle condition must be established for such cases. | 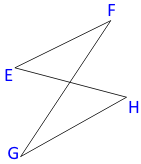 |
|
| Figure B-2 Crossling Traverse |
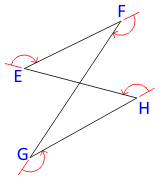
b. Deflection Angles
If deflection angles are used, the angle condition depends on how many times, if any, the traverse crosses itself.
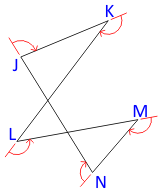 |
 |
|
| (a) Even crossings | (b) Odd crossings | |
| Figure B-3 Deflection Angles |
||
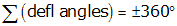 |
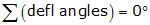 |
|
| Equation B-2 | Equation B-3 | |
Angle condition equations are exact so the 0°, 180°, and 360° in the equations are also exact.
c. Link Traverse
In order to determine angular misclosure for a closed link traverses, directions must be known at both ends:
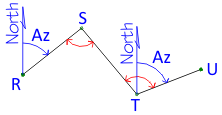 |
| Figure B-4 Link Traverse Angle Condition |
This isn't the case for most link traverses, even those which begin and end on known points. Since it can't be identified, potential angular misclosure is addressed in the traverse adjustment.
2. Angular Misclosure
Angular misclosure is the difference between the measured angles' sum on a traverse and the angle condition for the traverse configuration.
The amount of allowable angular misclosure is dependent on the survey purpose. The limits are generally expressed as an Error of a Series:
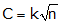 |
Equation B-4 | |
| C: Allowable misclosure, seconds k: expected error in each angle, seconds n: number of angles |
||
Traditional formal standards from the FGCS Standards and Specifications for Geodetic Control Networks are:
| Table B-1 | ||
| Angular Misclosure | ||
| Order | Class | k (sec) |
| First | - | 1.7 |
| Second | I | 3.0 |
| II | 4.5 | |
| Third | I | 10.0 |
| II | 12.0 | |
Example
What is the allowable angular misclosure for a five-sided traverse if it is to meet Second Order Class II standards, Figure B-5?
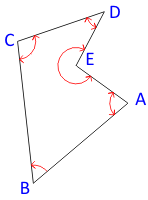 |
| Figure B-5 Allowable Misclosure |
From Table 1, k = 4.5". Substituting into Equation B-4:
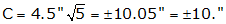
Because this is a five-sided loop traverse, using Equation B-1 the angles should sum to:
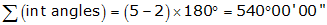
Therefore, the total should be in the range 539°59'50" to 540°00'10".
Informal standards can be created which reflect equipment, experience, conditions, project needs, etc.
Example
A control network is to be established for a construction project. Sight distances will be relatively short (under 300 ft) so measuring angles consistently will be a challenge. Testing under these conditions, our survey crew was able to measure an angle to a consistency of ±0°00'12". For this project, we will use an allowable misclosure of:
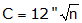
3. Angular Misclosure Distribution
Normally, the first step in traverse computations is distribution of the angular misclosure in order to meet the angular condition. This is referred to as angle adjustment. If performing a least squares traverse adjustment, angles are not adjusted since the angular misclosure is part of the overall adjustment.
Because angular misclosure is due to random errors, a distribution method which approximates their behavior would be the best to use. There are a few simplified methods which can be applied, each having advantages and disadvantages, Table B-2:
| Table B-2 | |||
| Method | Process | Advantage | Disadvantage |
|
Don’t distribute |
- - |
Simple; Can be replicated. |
Unless using a least squares adjustment, this method does not try to reconcile error accumulation. |
|
Arbitrary |
Put all error into random angle. |
None. |
Doesn't model errors well; Difficult to replicate. |
|
Equal distribution |
Apply equal correction to each angle. |
Simple; Can be replicated. |
Assumes error is same in each angle; Can imply incorrect angle accuracy. |
|
Judgment |
Apply different corrections to each angle depending on measurement repetition and conditions. |
Relatively simple; Better error modeling. |
Requires direct knowledge of measurement conditions. |
Why isn't Least Squares listed as a distribution method? Because angles aren't adjusted separately when a traverse is adjusted by least squares: angles and distances are adjusted simultaneously.
One thing we do not base corrections on is angle size. An angle is the difference between a total station’s initial and final readings; size of the angle has no impact on its error.
Example
Given the following traverse and measured angles:
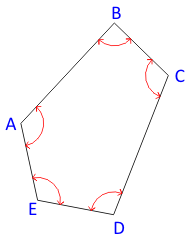 |
|
||||||||||||||
| Figure B-6 Example Angle Adjustment |
|||||||||||||||
The angle condition from Equation B-1 is
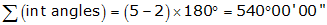

Since the angle total is short of the angle condition, corrections must be added.
Using an Equal Distribution
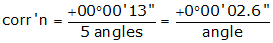
Apply correction:
|
Point |
Angle |
corr’n |
Corr’d Angle |
|
A |
125°30'20" |
+0°00'02.6" |
125°30'22.6" |
|
B |
88°21'31" |
+0°00'02.6" |
88°21'33.6" |
|
C |
112°38'35" |
+0°00'02.6" |
112°38'37.6" |
|
D |
104°21'40" |
+0°00'02.6" |
104°21'42.6" |
|
E |
109°07'41" |
+0°00'02.6" |
109°07'43.6" |
|
sums: |
539°59'47" |
+0°00'13.0" |
540°00'00.0" |
|
check |
check |
While the corrected angles total the angle condition, each is shown to 0.1" which implies a higher accuracy than shown in the original angles. But rounding each to the nearest second raises the total to 540°00'05".
Using Judgment
In this case, we take into account measurement conditions.
Consider point E, which has short sights on both sides. Shorter sights generally have higher pointing errors (given same target sizes).
Also, the field crew reported larger repeated direct and reverse angle spreads at point C.
The equal distribution’s correction was +0°00'02.6" per angle. We can drop that to +0°00'02" per angle for our three strongest angles (+0°00'06" total) and divide the remaining 0°00'07" among the two weaker ones.
|
Point |
Angle |
corr’n |
Corr’d Angle |
|
A |
125°30'20" |
+0°00'02" |
125°30'22" |
|
B |
88°21'31" |
+0°00'02" |
88°21'33" |
|
C |
112°38'35" |
+0°00'04" |
112°38'39" |
|
D |
104°21'40" |
+0°00'02" |
104°21'42" |
|
E |
109°07'41" |
+0°00'03" |
109°07'44" |
|
sums: |
539°59'47" |
+0°00'13" |
540°00'00" |
|
|
|
check |
check |
This takes into account individual conditions. The resulting angles do not imply accuracy beyond the original measurements.
Equal Distribution or Judgement?
Although an equal distribution can result in decimals beyond original accuracy, that's really not an issue. Why? Because balanced angles are an intermediate calculation so carrying additional digits reduces cumulative rounding error. In most simple traverse cases, an equal distribution works fine.
Distribution based on judgement should be used where there is personal knowledge of measurement conditions and angle certainty.