2. Field Variations
In all the methods discussed direction and/or distance measurements were made from both ends of the base line. In order to turn an angle from one end of the base line, the other end must be visible to serve as a back sight. In the field, this isn't always practical or efficient. The key to intersection solution is that the unknown point must be visible from both ends of the base line, or, conversely, the end points are visible from the unknown point. This allows the surveyor to make a single instrument set up - at the unknown point.
a. Determining instrument location
|
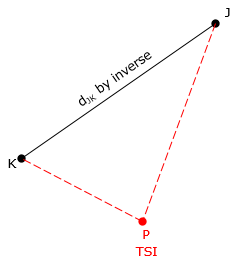
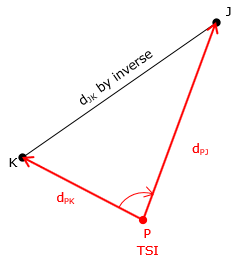
The base line still forms a known side of the triangle even if the end points are not inter-visible. That means two other measurements are necessary in order to fix the triangle. With a total station instrument (TSI) set up at the unknown point, Figure F-8, what measurements should be made? |
|
|
Figure F-8 |
|
|
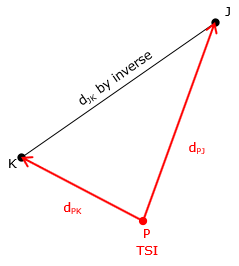
Distance-distance, Figure F-9
|
|
|
|
|
|
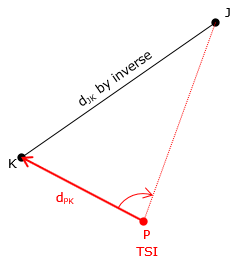
Distance-angle, Figure F-10
|
|
|
|
|
|
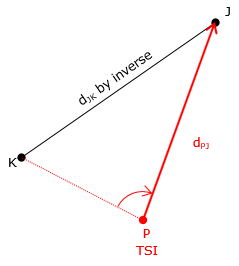
Angle-distance, Figure F-11
|
|
|
|
|
|
Distance-angle-distance, Figure F-12
|
b. Determining length of obstructed line
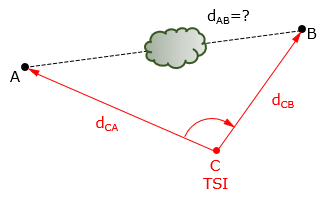
Sometimes it's not the TSI location that is desired, but the distance between two non-inter-visible points. For example, the sight between two adjacent property corners may be blocked due to intermediate obstacles such as trees. The surveyor, however, can find a TSI location from which both points can be seen. The distances to and angle between the points can be measured from the TSI, Figure F-13.
|
|
|
Figure F-13 |
This is called the missing line method since the desired line cannot be directly measured. Two distances and one angle measured are three elements of the triangle. The missing distance can be calculated using the Law of Cosines.
c. Leave it to the instrument
Being instrument-centric procedures, most TSI have onboard computational routines for instrument location and missing line determination providing sufficient measurements are made.