3. Point-to-point computations
Point-to-point computations involve just two points
a. Forward Computation
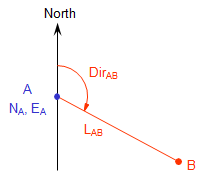
A Forward Computation is used to calculate a point's coordinates from another set of coordinates using distance and direction data between them, Figure A-8.
|
|
|
Equation A-1 |
|
|
Equation A-2 |
|
|
Figure A-8 |
|
|
Equations A-1 and A-2 are a combination of the latitude and departure and coordinate equations from the Traverse Computations chapter:
- North Lat is (+), South Lat is (–)
- East Dep is (+), West Dep is (–)
DirAB can be either a bearing or azimuth:
- If a bearing (0° to 90°) is used you must manually determine the correct algebraic sign for the Lat and Dep based on quadrant.
- Using azimuths (0° to 360°) automatically results in correct signs.
b. Inverse Computation
An Inverse Computation determines the distance and direction between two coordinate pairs, Figure A-9.
|
|
|
|
|
|
Equation A-3 |
|
|
|
Equation A-4 |
|
|
|
Equation A-5 |
|
|
|
Equation A-6 |
Coordinate differences, Δ’s, are the to point minus the from point: going from point C to point D means subtracting C's coordinates from D's.
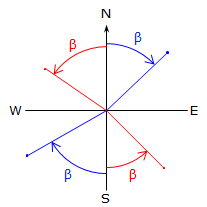
The algebraic sign on β and the resulting direction depend on the quadrant of the line. A positive angle is clockwise (to the right); a negative angle is counterclockwise (to the left). Both are from the north or south end of the meridian, Figure A-10.
|
|
|
Figure A-10 |
|
Table A-1 |
|||||
| Algebraic sign | Direction | ||||
| Quadrant | ΔN | ΔE | β | Bearing | Azimuth |
| NE | + | + | + | N β E | β |
| SE | - | + | - | S |β| E | 180°+β |
| SW | - | - | + | S β W | 180°+β |
| NW | + | - | - | N |β| W | 360°+β |
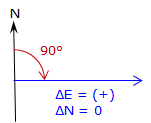
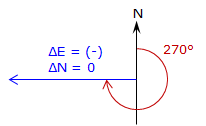
When ΔN = 0, Equation A-7 has no solution. Technically division by 0 is undefined, but actually the result of any number divided by 0 is infinity. So what does this mean? In surveying terms when ΔN = 0 the entire line length is ΔE resulting in a due East or West line, Figure A-11.
|
when ΔE is (+), Az = 90° |
when ΔE is (-), Az = 270° |
|
|
|
|
Figure A-11 |
|
If you check the tangent of 90° and 270° on your calculator you'll get either an error or "undefined" response. Try tan(89.99999°); you'll get a huge number. Tan(90°) = tan(270°) = infinity.
c. Examples
(1) Forward 1
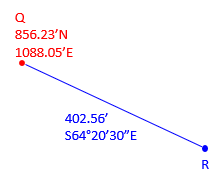
Compute the coordinates of point R given the information in Figure A-12:
|
|
|
Figure A-12 |
Because the bearing is South and East, the Lat is negative and Dep positive. From equations A-1 and A-2:
![]()
![]()
(2) Forward 2
Compute the coordinates of point R given the information in Figure A-13:
|
|
|
Figure A-13 |
Because the direction is an azimuth, Equations A-1 and A-2 will automatically compute the correct signs for the Lat and Dep.
![]()
![]()
(3) Inverse
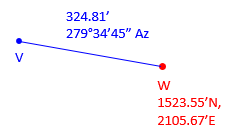
What are the lengtha and azimuth from point J to K?
| Point | North (ft) | East (ft) |
| J | 1153.65 | 704.08 |
| K | 988.85 | 200.75 |
Draw a sketch to visualize the line, Figure A-14.
|
|
|
Figure A-14 |
Substitute the coordinates into Equations A-3 and A-4 (remember, it's to minus from):
![]()
![]()
Use Equation A-5 to compute the length:
![]()
Compute β, the angle from the meridian:
![]()
Because ΔN is negative and ΔE is negative, the direction is in the South-West quadrant, so add 180° to β.
![]()