A. Coordinates
1. Coordinate System
A coordinate system is a datum for expressing point positions. The system consists of two or three reference axes perpendicular to each other.
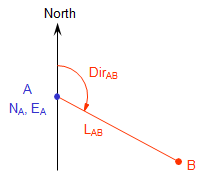
In a two dimensional system, one axis is oriented in the direction of a meridian defining North, the remaining axis being East, Figure A-1.
|
|
|
Figure A-1 |
In a three dimensional system, the third axis is oriented vertically, in the direction of elevation, Figure X-2.
|
|
|
Figure A-2 |
This section will deal primarily with two dimensional systems although the math involved can be easily expanded into the third dimension.
2. Positions
a. Absolute: Coordinates
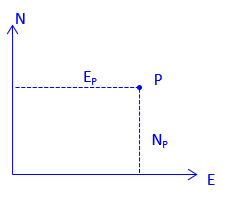
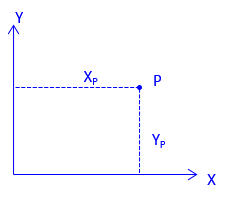
The absolute position of a point is expressed as coordinates which are perpendicular distances from the reference axes. In surveying and most mapping, the reference system uses North and East axes so position is expressed as (North, East) (aka, Northing and Easting), Figure A-3. Other applications, notably math, use X and Y axes; Y coinciding with the meridian. Positions are expressed as (X, Y), Figure A-4.
|
|
|
|
Figure A-3 |
Figure A-4 |
Caution must be exercised when using coordinates provided by others. Are (2000 ft,1000 ft) North-East or X-Y coordinates? A common error when importing coordinates in software is reversing their order: this flips and rotates the positions. This effect is demonstrated in Figures A-5 and A-6. The former uses coordinates in (N, E) order while the latter in (X, Y).
|
|
|
|
Figure A-5 |
Figure A-5 |
We will use the North-East coordinate form unless otherwise specified.
b. Relative
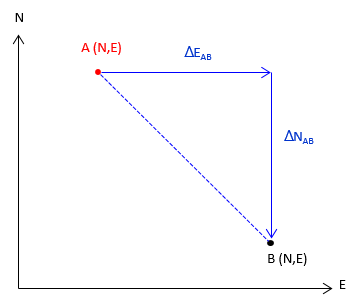
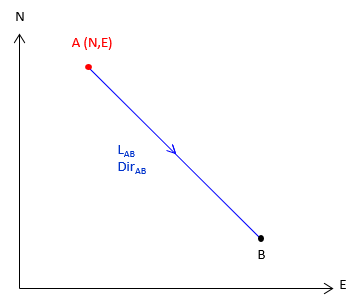
A relative position is where one point is with respect to another. This can be expressed as coordinate differences, Figure A-6, or as distance and direction, Figure A-7.
|
|
|
|
Figure A-6 |
Figure A-7 |
3. Point-to-point computations
Point-to-point computations involve just two points
a. Forward Computation
A Forward Computation is used to calculate a point's coordinates from another set of coordinates using distance and direction data between them, Figure A-8.
|
|
|
Equation A-1 |
|
|
Equation A-2 |
|
|
Figure A-8 |
|
|
Equations A-1 and A-2 are a combination of the latitude and departure and coordinate equations from the Traverse Computations chapter:
- North Lat is (+), South Lat is (–)
- East Dep is (+), West Dep is (–)
DirAB can be either a bearing or azimuth:
- If a bearing (0° to 90°) is used you must manually determine the correct algebraic sign for the Lat and Dep based on quadrant.
- Using azimuths (0° to 360°) automatically results in correct signs.
b. Inverse Computation
An Inverse Computation determines the distance and direction between two coordinate pairs, Figure A-9.
|
|
|
|
|
|
Equation A-3 |
|
|
|
Equation A-4 |
|
|
|
Equation A-5 |
|
|
|
Equation A-6 |
Coordinate differences, Δ’s, are the to point minus the from point: going from point C to point D means subtracting C's coordinates from D's.
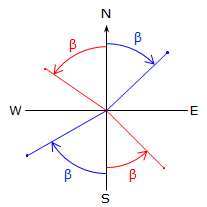
The algebraic sign on β and the resulting direction depend on the quadrant of the line. A positive angle is clockwise (to the right); a negative angle is counterclockwise (to the left). Both are from the north or south end of the meridian, Figure A-10.
|
|
|
Figure A-10 |
|
Table A-1 |
|||||
| Algebraic sign | Direction | ||||
| Quadrant | ΔN | ΔE | β | Bearing | Azimuth |
| NE | + | + | + | N β E | β |
| SE | - | + | - | S |β| E | 180°+β |
| SW | - | - | + | S β W | 180°+β |
| NW | + | - | - | N |β| W | 360°+β |
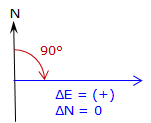
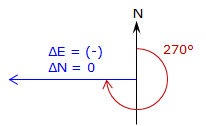
When ΔN = 0, Equation A-7 has no solution. Technically division by 0 is undefined, but actually the result of any number divided by 0 is infinity. So what does this mean? In surveying terms when ΔN = 0 the entire line length is ΔE resulting in a due East or West line, Figure A-11.
|
when ΔE is (+), Az = 90° |
when ΔE is (-), Az = 270° |
|
|
|
|
Figure A-11 |
|
If you check the tangent of 90° and 270° on your calculator you'll get either an error or "undefined" response. Try tan(89.99999°); you'll get a huge number. Tan(90°) = tan(270°) = infinity.
c. Examples
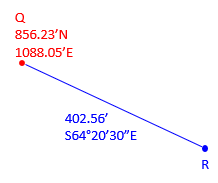
(1) Forward 1
Compute the coordinates of point R given the information in Figure A-12:
|
|
|
Figure A-12 |
Because the bearing is South and East, the Lat is negative and Dep positive. From equations A-1 and A-2:
![]()
![]()
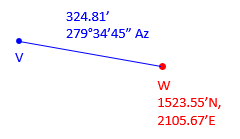
(2) Forward 2
Compute the coordinates of point R given the information in Figure A-13:
|
|
|
Figure A-13 |
Because the direction is an azimuth, Equations A-1 and A-2 will automatically compute the correct signs for the Lat and Dep.
![]()
![]()
(3) Inverse
What are the lengtha and azimuth from point J to K?
| Point | North (ft) | East (ft) |
| J | 1153.65 | 704.08 |
| K | 988.85 | 200.75 |
Draw a sketch to visualize the line, Figure A-14.
|
|
|
Figure A-14 |
Substitute the coordinates into Equations A-3 and A-4 (remember, it's to minus from):
![]()
![]()
Use Equation A-5 to compute the length:
![]()
Compute β, the angle from the meridian:
![]()
Because ΔN is negative and ΔE is negative, the direction is in the South-West quadrant, so add 180° to β.
![]()