Page 6 of 8
6. Comparing Different Measurement Sets
Two survey crews measure different horizontal angles multiple times; their results are shown in the table.
| Crew A | Crew B | |
| 2 D/R | 4 D/R | |
| Average Angle | 128°18'15" | 196°02'40" |
| Std Dev | ±00°00'12" | ±00°00'14" |
D/R means to measure an angle direct and reverse; each D/R set is 2 measurements
Which crew has better precision?
Crew A because their standard deviation is smaller.
Which crew has better accuracy?
We need to determine the expected error in each crew’s average angle. Use Equation F-4.
| Crew A: | 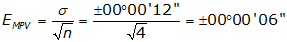 |
| Crew B: | 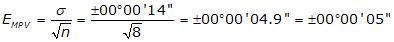 |
Crew B has better accuracy since the expected error in their average angle is less.