Page 4 of 8
4. The Danger of Including Mistakes
Let’s include a measurement with a mistake and see what happens.
Make the first measurement 46.66, an error of 1.00 units.
| num | value | v=meas=MPV | v2 |
| 1 | 46.66 | 46.66-45.912 = +0.748 | 0.559504 |
| 2 | 45.66 | 45.66-45.912 = -0.252 | 0.063504 |
| 3 | 45.68 | 45.68-45.912 = -0.232 | 0.053824 |
| 4 | 46.65 | 45.65-45.912 = -0.262 | 0.068644 |
| sums | 183.65 | 0.745476 |
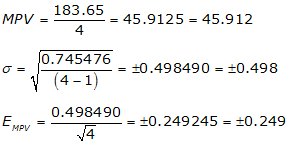
Note how large the standard deviation and EMPV error become. That’s because both are affected by the huge increase in the residuals caused by pushing parts of the 1.00 unit error into all of them. Including a measurement with a mistake degrades the rest of the measurements.
Always: get rid of mistakes before trying to analyze random errors.