b. Traverse with Azimuths
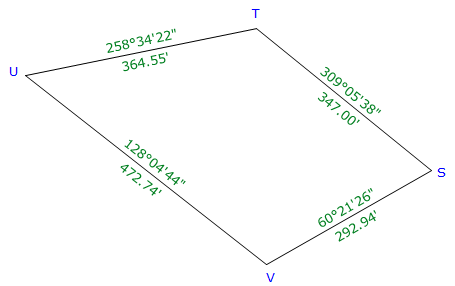 |
| Figure E-7 Azimuth Traverse Example |
| Line | Azimuth | Length (ft) | Lat (ft) | Dep (ft) |
| ST | 309°05'38" | 347.00 | +218.816 | -269.311 |
| TU | 258°34'22" | 364.55 | -72.226 | -357.324 |
| UV | 128°04'44" | 472.74 | -291.560 | +372.123 |
| VS | 60°21'26" | 292.94 | +144.885 | +254.602 |
| sums: | 1477.23 | -0.085 | +0.090 | |
| Distance | Lat err too far S |
Dep err too far E |
(1) Adjust the Lats and Deps
Setup Equations E-1 and E-2:
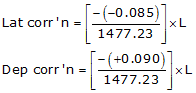
Solve Equations E-3 and E-4 for each line:
Line ST
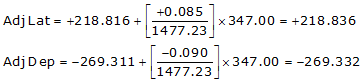
Line TU
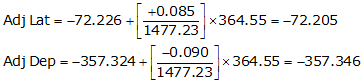
Line UV
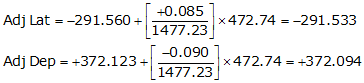
Line VS
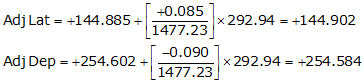
Check the closure condition
| Adjusted | ||
| Line | Lat (ft) | Dep (ft) |
| ST | +218.836 | -269.332 |
| TU | -72.205 | -357.346 |
| UV | -291.533 | +372.094 |
| VS | +144.902 | +254.584 |
| sums: | 0.000 | 0.000 |
| check | check | |
(2) Compute adjusted lengths and directions
Use Equations E-5 and E-6 along with Figure E-5 to compute the new length and direction for each line.
Line ST
Adj Lat = +218.836 <- North
Adj Dep = -269.332 <- West
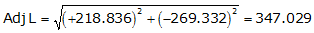
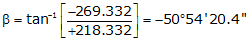
Because it's in the NW quadrant: Az = 360°00'00"+(-50°54'20.4") =309°05'39.6"
Line TU
Adj Lat = -72.205 <- South
Adj Dep = -357.346 <- West
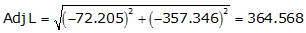
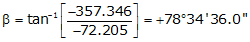
Because it's in the SW quadrant: Az = 180°00'00"+(78°34'36.0") = 258°34'36.0"
Line UV
Adj Lat = -291.533 <- South
Adj Dep = +372.094 <- East
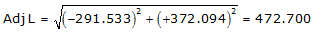
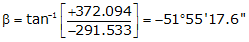
Because it's in the SE quadrant: Az = 180°00'00"+(-51°55'17.6") = 128°04'42.4"
Line VS
Adj Lat = +144.902 <- North
Adj Dep = +254.584 <- East
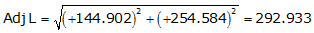
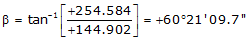
Because it's in the NE quadrant: Az = 60°21'09.7"
(3) Adjustment summary
| Adjusted | Adjusted | |||
| Line | Lat (ft) | Dep (ft) | Length (ft) | Azimuth |
| ST | +218.836 | -269.332 | 347.029 | 309°05'39.6" |
| TU | -72.205 | -357.346 | 364.568 | 258°34'36.0" |
| UV | -291.533 | +372.094 | 472.700 | 128°04'42.4" |
| VS | +144.902 | +254.584 | 292.933 | 60°21'09.7" |