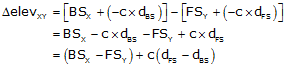3. Collimation

a. Description

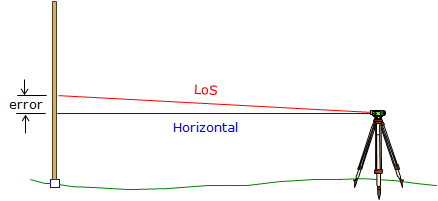
On an adjusted instrument which is correctly set up, the LoS should be horizontal and perpendicular to the instrument's VA. A non-horizontal LoS means the instrument has a collimation error. A LoS that is inclined or depressed from horizontal, Figure F-5, introduces a rod reading error.

Figure F-5 Collimation Error

Collimation error is caused by the vertical position of the crosshairs: if they are too low then the LoS is inclined; if they are too high, the LoS is depressed.

b. Check

(1) Procedure

Because collimation error cancels if BS and FS distances are balanced, checking for it purposely uses unbalanced sight distances. The elevation difference between two points is determined using a short BS / long FS condition followed by a long BS / short FS condition. If there is a collimation error, the two elevation differences will not be the same.

Because collimation error is a function of distance, the sight length for each reading is needed. The error is then stated as ratio (e.g. ft/ft) or angle above (+) or below (-) horizontal.

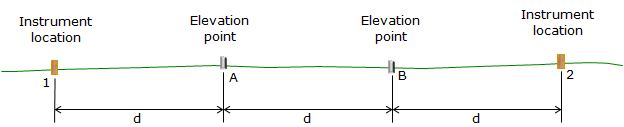
A baseline which consists of four roughly evenly spaced points is established. The points should be on an approximately straight line and placed at a uniform interval of 75 to 100 ft, Figure E-6. Points 1 and 2 are instrument locations and are marked with wooden stakes; Points A and B are elevation points and are marked with stable pins.

Figure F-6 Baseline

The instrument is set up at point 1 (it does not have to be exactly over the point).

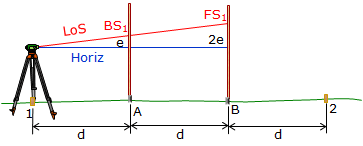
A short BS reading is taken on point A and a long FS reading on point B, Figure F-7

Figure F-7 First Setup at Point 1

The instrument is moved to point 2 (again, it does not have to be exactly over the point).

A long BS reading is taken on point A and a short FS reading on point B, Figure F-8

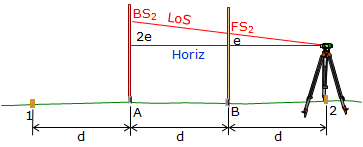Figure F-8 Second Setup at Point 2

The elevation difference point A to point B is:

from Point 1: BS₁ – FS₁

from Point 2: BS₂ – FS₂

If the two elevation differences are identical, the instrument is in adjustment. If they differ, the instrument has a collimation error.

Including the collimation error, e, in the elevation differences:

from Point 1: (BS₁ – e) – (FS₁ – 2e)

from Point 2: (BS₂ – 2e) – (FS₂ – e)

Setting the two differences equal and solving for e:

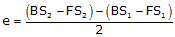Equation F-1

e is the total vertical error in a horizontal sight distance of d. Collimation error can be expressed as a vertical/horizontal ratio, Equation E-2, or angle, Equation E-3.

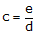	Equation F-2
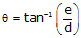	Equation F-3

Both equations require the average distance, d.

Rather than set the four points accurately at an interval of d, it is easier to set them at the approximate interval and then measure the distances as the readings are made. This is done by Three-Wire Leveling.

The distances from point 1 to A and B and from point 2 to A and B are determined by stadia. The measurements are used to compute an overall average distance, d, Figure F-9, and Equation F-4.

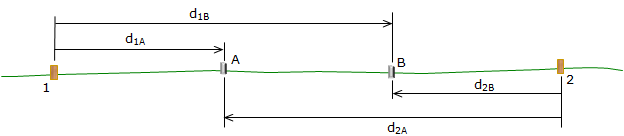Figure F-9 Base Line Point Spacing

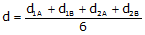		Equation F-4

Besides facilitating distance determination, reading all three horizontal crosshairs provides a check on the rod reading and allows carrying an additional decimal place. Refer to Topic Elevation Determination G. Three-Wire Leveling for a procedure description.

(2) Sample data sheet

Because each BS and FS consists of three rod readings and distances are computed as well as elevation differences, it can be quite easy to get lost in the process. To help, the following data sheet can be used to record readings and perform the collimation computations both as a ratio (c) and vertical angle (θ).

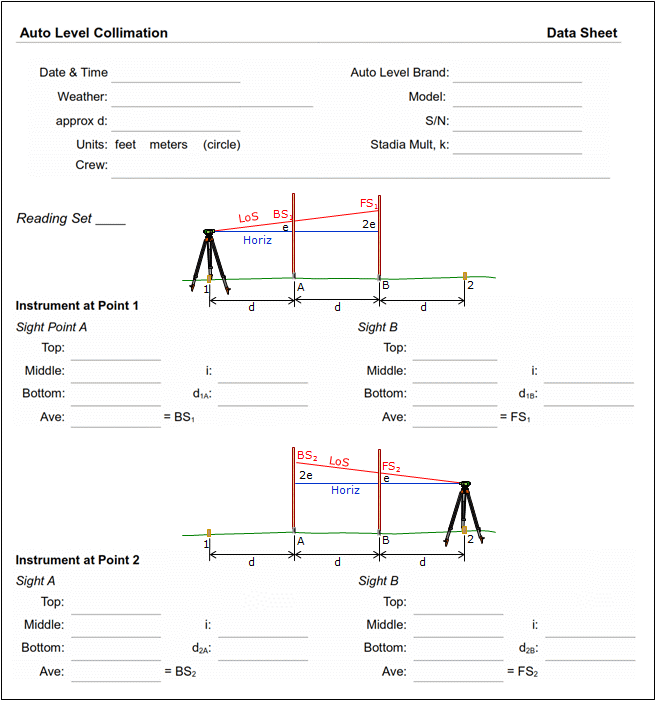
For a full-size pdf version click here; for a spreadsheet template click here.

A collimation check example using this data sheet will be shown shortly.

(3) How much is acceptable?

Table F-1 shows the maximum allowable instrument collimation error for First, Second, and Third Order leveling.

Table F-1

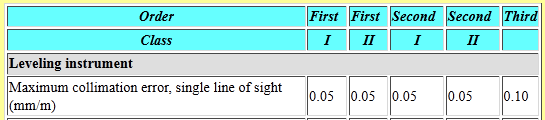From Section 3.5 Geodetic Leveling of Standards and Specifications for Geodetic Control Networks, FGCC, 1984

The Standards and Specifications... also state that "Compensator-type instruments should be checked for proper operation at least every 2 weeks of use."

While these are control-level standards, they can serve as a guide for local applications. Local project control might use Third (or possibly Second) Order specifications while that for topographic control would be looser. Regardless, the error in an instrument is not known unless a collimation check is performed.

c. Compensation

(1) Procedure

For most leveling projects, collimation error can be removed by balancing BS and FS distances, that is, making them equal.

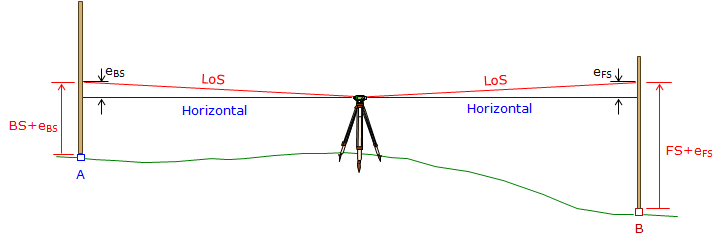Figure F-10

If the BS and FS distances are equal, Figure E-16, then the reading error in both will be the same: e_BS=e_FS. Because Elev_B = Elev_A + BS - FS, the BS error (e_BS) is added and the FS (e_FS) error is subtracted so the collimation error cancels. That means that the elevation of B is correct with respect to A if the BS and FS distances are equal. However, the EI is incorrect since it is subject only to the BS error. That's why in differential leveling we have one BS and one FS per setup and make sure their distances are approximately equal.

(2) Mathematic

Whenever the level is used, the correction could be applied to each reading made, Figure F-11.

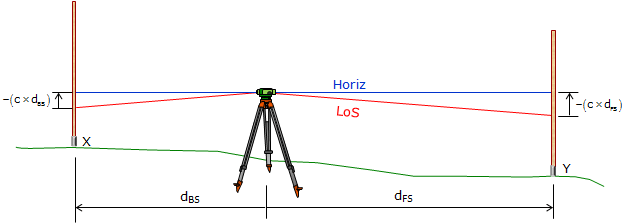Figure F-11 Unbalance Sight Distances

The collimation error is compensated by multiplying the correction by the BS and FS length difference and adding it to the elevation difference.

This requires the length of each sight be captured as the readings are taken. This is the case when Three-Wire Leveling but generally not so when doing basic differential leveling using only the center hair unless paces are counted and recorded.

(3) Adjustment

The reticule adjusting screws are located near the eyepiece under a cover. Removing the cover reveals the adjusting screws at the top and possibly bottom of the reticule (there might also be side adjusting screws but they aren't necessary for this adjustment), Figure F-12.

Figure F-12 Reticule Adjusting Screws

If there is an upper and lower screw, then one must be first loosened and the other then tightened to move the crosshairs.

If there is only a single screw then only that screw is loosened or tightened.

How far to move the crosshairs?

For the previous example, we know that the total error in the BS from point 2 to A is: (152 ft)x(-0.0000266 ft/ft) = -0.004 ft.

The correct BS reading should be 5.540+0.004 = 5.544 ft

That means to remove the collimation error, we would use the adjusting screws to raise the crosshairs to a 5.544 ft BS reading.

Hmm... trying to see 0.004 ft at 152 ft... not too easy.

Probably best to leave the crosshairs alone and use one of the other two methods.