A. Definitions
1. Meridian
A meridian is a north-south reference line. It is used as a basis for a direction, which describes a line’s orientation.
Common meridians include, but are not limited to, Figure A-1:
|
|
|
| Figure A-1 Meridians |
||
`
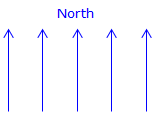
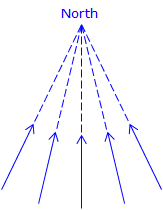
Depending on the system, meridians may converge or may stay parallel, Figure A-2.
|
|
|
| (a) Parallel | (b) Converging |
|
Figure A-2 |
|
Plane Surveying: Parallel meridians are typical in Grid and Assumed systems. For small project areas such as a single lot survey, meridians can assumed to be parallel, regardless of system, without introducing significant error.
Geodetic Surveying: In a larger earth-based system meridians converge to a point (e.g., North Pole).
Most meridian systems (even Assumed) are constant over time. However, magnetic meridians change location and their change is not consistent. Magnetic meridians are important as the first instrument extensively used for property surveys was the compass. Although True directions were reported in the early Public Land Surveys, they were first measured by compass then converted using solar observation.
A surveyor will select an appropriate meridian for the project at hand and orient all survey lines to it. Sometimes directions based on one meridian must be converted to a different meridian in order to maintain consistency across surveys. We’ll look at that, along with magnetic direction conversions, in Meridian Conversions later.
We will use parallel meridians for the remainder of this discussion - convergency issues will be covered in a later Topic.
2. Direction
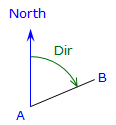
A direction is angle from a meridian to a line. It is similar to a horizontal angle in a traverse except the backsight is always along the meridian, Figure A-3.
|
|
|
Figure A-3 |
There are two different ways to express line direction: bearing and azimuth.
a. Bearing
A bearing is an angle from the North or South end of the meridian turned to the East or West. A bearing has three parts:
- Prefix - N or S indicating which end of the meridian is turned from.
- Angle
- Suffix - E or W indicating turning direction from the meridian to the line.
N 66°40' E - from the North end of the meridian, turn 66°40' to the East.
Example
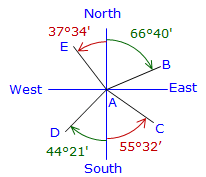 |
Bearing AB = N 66°40' E Bearing AC = S 55°32' E Bearing AD = S 44°21' W |
| Figure A-4 Bearings |
A bearing falls in one of four quadrants so the angle does not exceed 90°. The angle is to the right (clockwise) in the NE and SW quadrants, to the left (counter-clockwise) in the SE and NW quadrants. A due North direction can be expressed as either N 00°00' E or N 00°00' W; due East as N 90°00' E or S 90°00' E; similarly for dues South and West.
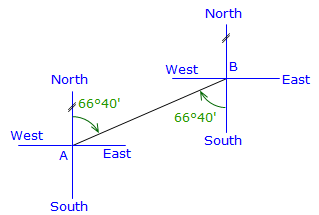
A back-bearing is reverse of a bearing, that is, Bearing BA is the back-bearing of Bearing AB. Because the meridians are parallel at both ends of the line, the bearing angle is the same but quadrant is reverse. This is true only when meridians are parallel. Where meridians converge, the forward and back bearing angles will differ by the total convergence. More on this later.
|
|
Bearing AB = N 66°40' E
|
| Figure A-5 Back Bearing |
b. Azimuth
An azimuth is an angle to the right (clockwise) from the meridian to the line. In most cases the azimuth is turned from the north meridian end; earlier control surveys used the south end. An azimuth varies from 0° to 360°.
Example
|
|
Azimuth AB = 66°40' Azimuth AC = 124°28' Azimuth AD = 224°21' Azimuth AE = 322°26' |
| Figure A-6 Azimuths |
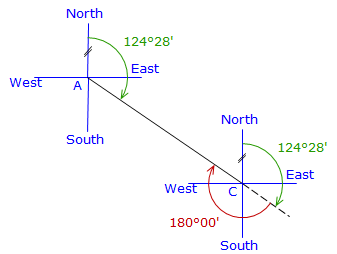
A back-azimuth is reverse of a azimuth: Azimuth CA is the back-azimuth of Azimuth AC. Because the meridians are parallel at both ends of the line, the back-azimuth and forward azimuth differ by 180°. As with bearings, this is true only when meridians are parallel. Where meridians converge, the forward and back azimuths will differ by (180° ± total convergence). More on this later.
Example
|
|
Azimuth AC = 124°28' Azimuth CA = 124°28' + 180°00' = 304°28' |
|
Figure A-7 |
3. Converting Between Bearings and Azimuths
Since Bearings and Azimuths are both referenced to a meridian it is simple to convert one to the other.
To convert from bearings to azimuths:
| Table A-1 | ||
| Quadrant | From Bearing | To Azimuth |
| NE | N β E | β |
| SE | S β E | 180° - β |
| SW | S β W | 180° + β |
| NW | N β W | 360° - β |
Example
|
|
Azimuth AB = 66°40' Azimuth AC = 180°00' - 55°32' = 124°28' Azimuth AD = 180°00' + 44°21' = 224°41' Azimuth AE = 360°00' - 37°34' = 322°26' |
| Figure A-8 Azimuths from Bearings |
To convert from an azimuth, α, to a bearing:
| Table A-2 | |
| Quadrant | To Bearing |
|
NE |
N α E |
|
SE |
S (180° - α) E |
|
SW |
S (α - 180°) W |
|
NW |
N (360° - α) W |
Example
|
|
Bearing AB = N 64°40' E Bearing AC = S (180°00'-124°28') E = S 55°32' E Bearing AD = S (224°21' - 180°00') W = S 44°21' W Bearing AE = N (360°00' - 322°26') W = N 37°34' W |
|
Figure A-9 |
Rather then memorize tables, drawing a sketch will help determine correct conversion logic to use.