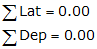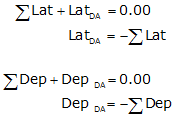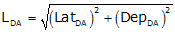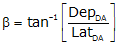J. Forcing Closure

1. General

Forcing closure means to take an open link traverse, Figure I-1, and create a closed loop traverse by connecting the end points.

While this does result in a perfectly closed traverse it cannot account for any errors in the original open link. Forcing closure is commonly applied to initially map a property description whose last course reads similarly to "thence back to the point of beginning." A description like this is open since it does not specify length or direction of the closing line.

2. Procedure

An open traverse< Figure I-2, is closed by making it meet the closure condition:

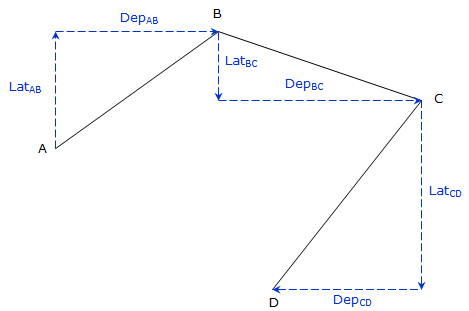
When the latitudes and departures are added, the amount by which they don't equal zero are the latitude and departure of the closing line, Figure I-3.

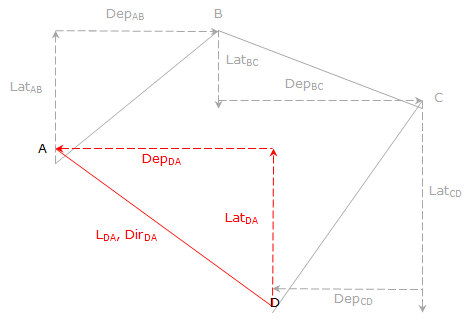
Once the latitude and departure of the closing line are determined, its length and direction can be computed from equations we've used before:

The mathematical signs on the closing latitude and departure determine in which quadrant the line is.

3. Example

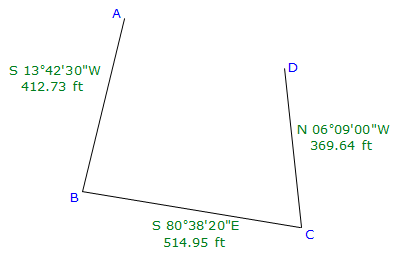
Determine the closing line's length and direction for the open traverse shown in Figure I-4.

a. Compute the latitudes and departures of the traverse lines

b. Sum the latitudes and departures

c. Determine the latitude and departure for the closing line

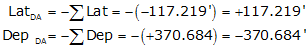
d. Then its length and direction

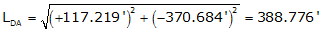
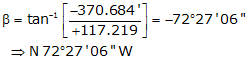
4. Summary

Forcing closure should never be done instead of closing a traverse using measurements or known endpoints. Being able to compute a missing line is no substitute for measuring it since errors can't be isolated. In the above example, if the length of line BC was mis-recorded as 514.95 instead of 541.95 that error won't be discovered but the traverse could still be forced to close. The length and direction of the closing line are dependent on, and absorb, all measurement errors and mistakes.