B. Significant Figures
1. Definition
In each of our taping examples, we stated the measurement to the smallest marked division on the tape and then interpolated the next digit. For example, we reported 9.83 ft with a tape divided to tenths, Figure B-1:
 |
| Figure B-1 Measurement Interpolation |
When we report a measurement, we’re conveying its magnitude (size) and resolution (which can imply accuracy). We do this using significant figures (sig fig). The number of sig fig in a number is all the digits of which we’re certain plus an additional estimated digit. Our 9.83 ft distance has three sig fig.
2. Zeros
Most of the confusion with sig fig centers on zeros (0). There are times when a 0 is significant, and other times when it is merely a placeholder. For example, do the following two distances mean the same thing?
200.00 ft
200 ft
Both express the same magnitude, but they differ in resolution. 200.00 implies a resolution to 0.01 (good to the nearest hundredth). How about 200? Is its resolution 1, 10, or 100?
The rules for zeros are:
(1) Zeros between nonzero digits are significant: 203 30501
(2) Zeroes to the left of a measurement are not significant: 00
5 00.0025
(3) Zeroes to the right of a measurement are only significant if a decimal point also appears in the quantity: 82.0 15.3600
Although these cover most situations, there can still be confusion when encountering zeros. How many sig fig does 200 have? According to the rules, both zeros would be merely place holders indicating magnitude but not accuracy, so 200 would have 1 sig fig.
But what if both zeros are significant (e.g., distance measure to the nearest foot)? How do we write 200 to show 3 sig fig?
One way would be to include a bar ( ¯ ) over the last significant 0:
![]()
The disadvantage to this is that most people interpret a bar over a number as an infinitely repeating digit. It’s also sometimes hard to see. On top of that, how do you enter that on a computer keyboard?
Another would be to place a decimal point after the second 0: 200.
Unfortunately the decimal point often gets “lost” when people look at the number. Or more often, we just leave it off.
The best way is to express the number in scientific notation: 2.00x102
2.00 is the coefficient and is the number subject to error. This uses the last rule of zeros - zeros to the right of the decimal point are significant.
102 is the base and is an exact multiplier (100 exactly).
What if the first zero (the one immediately after the 2) is significant and the second is a place holder? How would you record it showing 2 sig fig?
A bar over the first 0 making it significant, or,
2.0x102 using scientific notation.
3. Examples
How many sig fig in each of these numbers?
| Number | Number | Number |
| 4.90 | 0.00120 | 0.001060 |
| 56.0020 | 000200.000 | 780. |
| 0.0018 | .0018 | 1.8x10-3 |
Want to see the answers? Click here.
4. Error-Free numbers
There are two particular categories of numbers which are error free and therefore have an infinite number of sig fig. Using these numbers does not introduce any error beyond what is already in the measurement.
- Counts - These are whole integers and represent “how many” of something. If we measure an angle twice direct and reverse there are a total of 4 measurements: 4 exactly, not 3.99 or 4.01.
- Many conversion factors - These allow us to convert a measurement from one unit to another without introducing error. There are exactly 12 inches in exactly 1 foot. There are exactly 43560 sq ft in exactly 1 acre. As mentioned above, when using scientific notation the base is also exact.
5. Math operations
Measurements are often combined with other measurements to compute different quantities. It is sometimes a challenge to determine how many sig fig there should be in the computed quantity. To help, we have a few rules.
a. Addition & Subtraction
The result has the same level of accuracy as the least accurate number. The number of sig fig in the result is independent of the number of sig fig in any of the addends.
Example: What is the sum of 56.35 + 105 + 0.25 + 256.35
The raw sum is 471.95
The least accurate number is 105 which is good to the nearest 1
Therefore, the sum expressed to the nearest 1 is 472
Think of it this way: It's about 154 miles from where I'm sitting to Miller Field in Milwaukee. If I move my chair one foot further away, I'm still about 154 miles away from Miller Field. I wouldn't say Miller Field is about 154 miles and one foot away. I can't can state a result any more accurately than my least accurate number.
b. Multiplication & Division
The result has the same number of sig fig as the least sig fig in either of the numbers being multiplied or divided.
Example: What is the product of 46.53 x 23.1?
The raw product is 1074.843
46.53 has 4 sig fig, 23.1 has 3 sig fig
Therefore, the product expressed to 3 sig fig is 1070
Note the left 0 is significant, the right 0 is not
Example: convert 2.54 acres to square feet
There are 43,560 sq ft in 1 acre; this is an exact conversion factor
2.54 acres x (43,560 sq ft / 1 ac) = 110,642.4 sq ft (raw)
Since 2.54 has 3 sig fig, the area is 111,000 sq ft
c. Chain calculations
Chain calculations use combinations of the add/subtract and multiply/divide rules. Intermediate values are often rounded when performing long calculations, but doing so can have a cumulative effect on the final answer. To minimize this effect, intermediate values should be carried with extra digits and rounding done just once- at the end.
Example 1
What is the volume in cubic meters of the cube shown in Figure B-2?
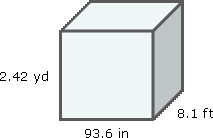 |
| Figure B-2 Volume of a Cube |
Volume of a cube is: 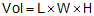
Metric conversion factor (international foot definition, exact): 2.54 cm = 1 in
Method 1
Convert each dimension to meters, each expressed to correct number of sig fig.
Exact conversion factors are shown in brackets [].
L=96.3 in ← 3 sig fig
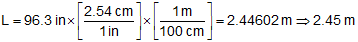
W=8.1 ft ← 2 sig fig
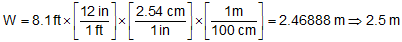
H=2.42 yd ← 3 sig fig
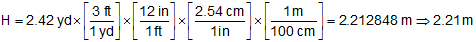
Compute the volume
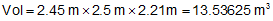
Since width, W, only has 2 sig fig, the volume is 14 m3
Method 2
Same as Method 1 except carry an additional sig fig for intermediate calculations.
From the previous computations: L=2.446 m; W=2.47 m; H=2.213 m
Compute the volume
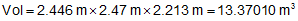
Since width, W, only has 2 sig fig, the volume is 13 m3
Carrying an additional sig fig for the intermediate calculations minimizes the cumulative rounding error. In this case, it affects the volume by one cubic meter (more than 7%).
Example 2
Convert 159°10'13" to decimal degrees with the correct number of sig fig.
This is an example of a single quantity (an angle) expressed in mixed units (deg, min, and sec). The initial inclination is to say there are 7 sig fig in the angle: 3 from the degrees plus 2 from the minutes plus 2 from the seconds. However that is incorrect.
- There are an infinite number of sig fig in the degrees portion - the angle contains exactly 159°. Any deviation from that is taken up in the minutes and seconds.
- There are an infinite number of sig fig in the minutes portion - the angle contains exactly 10'. Any deviation from that is taken up in the seconds.
- There are 2 sig fig in the seconds portion - it is the smallest unit and absorbs all the uncertainty in the degrees and minutes.
So how do we correctly convert mixed units to a single unit system?
Begin by converting all units to the smallest unit, the one subject to error: convert degrees and minutes to seconds
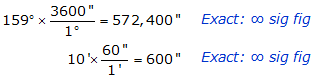
The conversion factors are exact so 572,400" and 600" are exact.
Add the angles part together in the smallest unit.
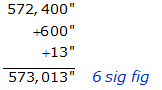
Because the deg and min are exact, the least accurate number is 13", good to the nearest second. That makes the sum good to 6 sig fig based on the addition rule.
Convert the sum to the final units
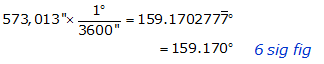
The conversion factor is exact. The final result should have the same number of sig fig as the sum from the previous step.
The angle correctly converted is 159.170° to 6 sig fig.
6. Sensitivity analysis
Sometimes chain calculations can be so long or complex that it’s hard to track sig fig through them. This is especially challenging when using software to determine results from combined measurements.
One way to get a feel for the accuracy of the result is to vary one or more of the measurements and see their effect on the result, that is, how sensitive the answer is to variation of the input.
Example 1
If rainfall intensity is 1.4 in/hr, what is the volume of water over a 2.3 acre field during a 20 minute storm? Compute in cubic yards to the correct number of sig fig.
Set up as one long computation making sure the units cancel correctly:

Figure out the sig fig in each of the numbers used:
1.4 in/hr 2 sig fig
20 min 1 sig fig ← least number of sig fig
2.3 acres 2 sig fig
all conversion factors are exact so each has infinite number of sig fig.
Since the least number of sig fig for any of the numbers is 1, the answer would also have just 1:
Vol = 100 yd3
If time is good to the nearest 10 minutes, then the volume is only good to the nearest 100 cubic yards.
Let's check this using a sensitivity analysis
20 min has one sig fig, that means that to the nearest 10 minutes the time was 20. In reality the time could have ranged between ~15 and ~25 minutes and still be 20 to the nearest 10 minutes. Notice that the range represents ±half the uncertainty:
±(half 10 minutes) = ±5 minutes
Numbers falling outside this range would not have been recorded as 20:
If real time were 14 minutes, it would have been recorded as 10.
If real time were 26 minutes, it would have been recorded as 30.
So varying time: 20 min
uncertainty is ±5 min
range is 15 to 25 min
| time (min) | raw vol (yd3) | raw vol is computed with extra dgiits |
| 15 | 108.2778 | |
| 20 | 144.3037 | range is ~72 yd3 |
| 25 | 180.3796 |
Notice at what level the volume is affected by varying the time within the uncertainty range. It’s constant at 100 yd3 level but not at the 10 yd3 level - the change is >50 yd3. This means you can’t reliably state the volume to the nearest 10 or 1 yd3 if time is measured only to the nearest 10 minutes.
What if we instead vary the rainfall intensity or the field area?
Rainfall intensity: 1.4 in/hr
uncertainty is ±0.05
range is 1.35 to 1.45 in/hr
| Intensity (in/hr) | raw vol (yd3) | |
| 1.35 | 139.1500 | |
| 1.4 | 144.3037 | range is ~10 yd3 |
| 1.45 | 149.4574 |
Area: 2.3 acres
uncertainty is ±0.05 acres
range is 2.25 to 2.35 acres
| time (min) | raw vol (yd3) | |
| 2.25 | 141.1667 | |
| 2.3 | 144.3037 | range is ~6 yd3 |
| 2.35 | 147.4407 |
Notice that the time uncertainty affects the final volume much more than the uncertainties in intensity or area. That means is if we need a more accurate volume, we should first increase time accuracy.
Example 2
Use a sensitivity analysis to convert 159°10'13" to decimal degrees with the correct number of sig fig.
Using our calculator DMS to Deg conversion button we get 159.17027778°
Since the estimated digit on the angle is in the seconds position, add and subtract 0.5" from the angle and compare those conversions.
| DMS | Deg | |
| subtract 0.5" | 159°10'12.5" | 159.17013889 |
| original angle | 159°10'13" | 159.17027778 |
| add 0.5" | 159°10'13.5" | 159.17041667 |
The three converted angles are consistent through the first three decimal places; they vary in the fourth. Within the range of uncertainty of the smallest unit, we would state the decimal equivalent of the angle is 159.170° to 6 sig fig. Notice that this is the same as we determined in the previous section.
7. Rounding Methods
Rounding becomes an issue when the next digit after the last to be kept is a 5. Computers and most people round up if the following digit is a 5 (this is the 4/5 rounding rule: 4 or less, leave alone; 5 or more, round up).
Example: 34.65 to 3 sig fig rounds to 34.7
This approach works well for most cases.
Surveyors, on the other hand, use an even rounding rule when the next digit is a 5;
- if the last digit to be kept is even, it is left as is,
- if the last digit to be kept is odd, it is increased to the next even.
Examples:
34.65 to 3 sig fig rounds to 34.6
18.215 to 4 sig fig rounds to 18.22
If you follow the surveyor’s rule, what about numbers which follow the 5?
For example how would you round 12.5496 to 2 sig fig?
Is .5496 greater than .5 so in this case we’d round to 13?
Remember what sig fig are: the digits of which we’re certain plus an estimate. The 5 isn’t a sig fig - the preceding digit is and that’s an estimate. We’re using the 5 to refine that estimate. The 5 is 10 times less significant than the estimate, the following 4 is 100 times less significant, and so on. Basically, anything after the 5 is garbage, noise, and can be ignored: key only on the 5.
Therefore, 12.5496 to 2 sig fig would round to 12.
So why do surveyors use this rule? Well, for many non-digital measuring devices, the smallest division can usually be estimated to 1/2. That means there’s a 50/50 chance of estimating incorrectly. If we always rounded up when encountering a 5 (the half-division), then the rounding would always be biased in one direction. By using the even rounding rule, sometimes we round up, sometimes down; in the end it evens out (we’re really quite a clever bunch).