Solution: Random Errors
Problem (1)
Survey Crew A measured a distance multiple times: 118.54', 118.52', 118.48', 118.54', 118.53', 118.47'.
Determine
The most probable line length
Its standard deviation
The length's expected error
Compute all to 0.001'.
-
Meas
v
v2
118.54
+0.027
0.000729
118.52
+0.007
0.000049
118.48
-0.033
0.001089
118.54
+0.027
0.000729
118.53
+0.017
0.000289
118.47
-0.043
0.001849
sums:
711.08
0.004734
Problem (2)
Two crews measured different distances multiple times. There results, in feet, are shown in the table below:
-
Crew A
Crew B
Num of meas
4
12
Average
87.96
108.53
Standard deviation
±0.030
±0.035
Which Crew had better:
Precision?
Crew A had better precision because its standard deviation was lower.
Expected accuracy?
Must compute and compare EMPV for each crew
Crew B had better expected accuracy since its EMPV was lower.
Problem (3)
The zenith angle to the top of a flag pole was measured with these results: 37°18'55", 37°19'04", 37°19'09", 37°18'53", 37°19'02"
Determine
The most probable zenith angle
Its standard deviation
The angle's expected error
Compute all to 0.1".
Subtract 37°18' from each angle to work with just seconds.
-
Angle
Sec
v
v2
37°18'55"
55
-05.6
31.36
37°19'04"
64
+03.4
11.56
37°19'09"
69
+08.4
70.56
37°18'53"
53
-07.6
57.76
37°19'02"
62
+01.4
1.96
sums:
303
173.20
Problem (4)
The length and width of a building are measured in feet, summarized in the table below.
What are the building's area and expected area error in square yards?
-
Length
v
v2
Width
v
v2
173.9
-0.33
0.109
89.6
-0.20
0.040
174.5
+0.27
0.073
90.1
0.30
0.090
174.3
+0.07
0.005
89.7
-0.10
0.010
sums:
522.7
0.187
269.4
0.140
The length sum has 4 sf, its average will have 4 sf.
The width sum has 4 sf, its average will have 4 sf.
Carry one more sf for each MPV to minimize intermediate rounding.
-
Length:
Width:
Each SD and EMPV are 3 sf, including an additional one for intermediate calculations.
Since length and width should both have 4 sf, Area = 5215 yd2.
Since additional sf were carried for L, W, and their EMPVs, the area error should be expressed to 2 sf: Error = ±10. yd2.
5215 yd2 ±10. yd2
Problem (5)
A lab technician was to determine the moisture content of a soil sample. She weighed the sample 4 times and obtained an average of 583.4 gr with a ±0.9 gr standard deviation. After the sample was dried for 24 hours at 400° F, she weighed it 6 times for an average of 552.9 gr and standard deviation of ±1.5 gr. What was the soil’s moisture content, and its expected error, in grams?
Because a subtraction is involved, must use Error of a Sum. Carry additional sf for the error comps.
30.5 gr ±0.8 gr
Problem (6)
Four different survey crews independently measured the elevation difference from point A to B. Because the have varying experience levels, not all the elevation differences are the same quality. Their results and expected uncertainties are listed in the table. What is the most probable elevation difference and its uncertainty?
Answer:
Weights are inversely proportional to standard deviation squared. Weight can be "normalized" by dividing all the raw weights by the smallest one.
| Crew | Elev Diff, m | σ | Wraw | W | W x m | v | v2 |
| 1 | -5.36 | ±0.05 | 400 | 5.76 | -30.87 | 0.01 | 0.0001 |
| 2 | -5.41 | ±0.08 | 156.25 | 2.25 | -12.17 | -0.04 | 0.0016 |
| 3 | -5.37 | ±0.04 | 625 | 9.00 | -48.33 | 0.00 | 0.0000 |
| 4 | -5.43 | ±0.12 | 69.44 | 1.00 | -5.43 | -0.06 | 0.0036 |
| Sums | 18.01 | -96.80 | 0.0053 |
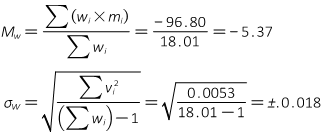
Elev Diff = -5.37 ft ±0.018 ft







