Self Study: Least Squares 5
Problem (1)
Determine the best-fit straight line equation for the data in the following table:
| X, m | Y, m |
| 10 | 300 |
| 14 | 190 |
| 20 | 100 |
Use any method you prefer.
Problem (2)
The shape of a freely hanging powerline between supports is a complex curve called a catenary. The catenary equation uses hyperbolic trigonometery to define the entire curve. A section of the curve can be closely approximated using a parabola, same as a vertical curve.
A powerline crossing a waterway has targets for monitiring purposes at approximately 74 ft spacing along the wire. The utility company wants to know the clearance between the line and the river at its Oridinary High Water Mark elevation of 1896.5 ft.
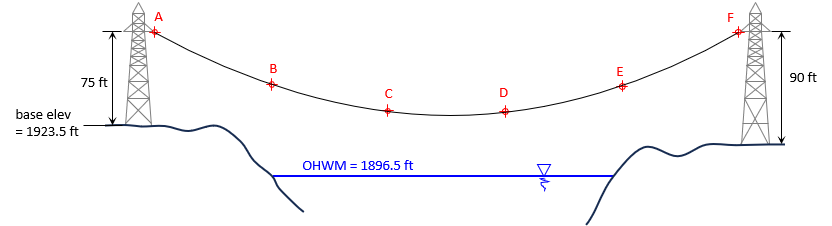
A surveyor established a baseline from which she was able to make sufficient measurements to determine the target poisitons. Using X for horizontal position and Y for vertical, she assumed X = 200.0 ft and Y = 1000.0 ft for point A. All target coordinates are listed in the table.
| Target | X | Y |
| A | 200.0 | 1000.0 |
| B | 274.3 | 966.7 |
| C | 347.7 | 950.2 |
| D | 422.3 | 949.6 |
| E | 496.5 | 965.6 |
| F | 570.1 | 1000.2 |
Part (a) What is the observation equation for target E?
Part (b) A least squares adjustment yielded these results:
| a | 0.001531 | |
| b | -1.18053 | |
| c | 1175.1 |
Using the information on the diagram and adjustment results, determine the minimum distance between the wire and river at OHWM.
Solutions: Least Squares 5