Solution: Least Squares 4
Statistics and Error ellipses
The following traverse was adjusted by least squares to determine the coordinates of points G and H.

Final coordinates of G and H are:
| Point | North | East |
| G | 4,958.913 | 917.702 |
| H | 5,067.094 | 1,252.311 |
Matrices from the final iteration of the adjustment are:
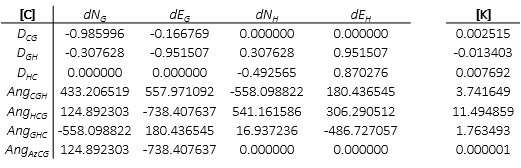


Compute:
(a) Expected uncertainties of the adjusted coordinates.
(b) Adjusted observations.
(c) Parameters of the standard and 95% CI error ellipsii at each adjusted point.
Solution
(a) Expected uncertainties of the adjusted coordinates.
Residuals are computed from [V] = [CU] - [K]
Since the [U] elements are all zero, [V] = -[K]

(b) Adjusted observations.
Add the [V] matrix elements to the corresponding field measurements to get the adjusted observations.
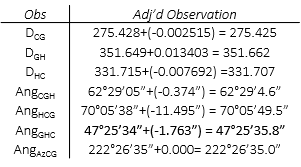
(c) Standard and 95% CI error eliipsii
Point G
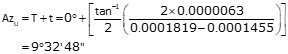

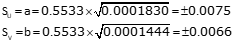
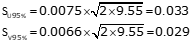
Point H
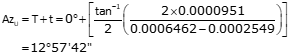

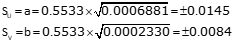
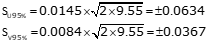
Error Ellipse Summary
| Std | 95% CI | ||||
| Point | AzU | a | b | a | b |
| G | 9°32'48" | 0.0075 | 0.0066 | 0.033 | 0.029 |
| H | 12°57'42" | 0.0145 | 0.0084 | 0.0634 | 0.037 |