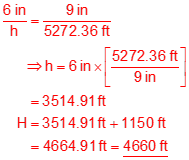Solution: Single Vertical Photo
Problem (1)
The photo scale at point G is 1"=200', at point H it is 1"=300'. Which point is at a higher elevation?
Scale is a function of elevation: the higher the point, the larger its scale. Because point G has the larger scale, it is at higher elevation..
Problem (2)
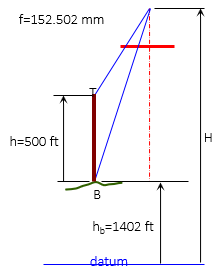
The top and bottom photo coordinates (x,y) of a 500 ft tall radio tower, in inches, are (-1.29,1.05) and (-0.89,-0.73). The tower base elevation is 1402 ft. The camera focal length was 152.502 mm. What was the flying height for the photo? Determine to nearest 10 ft.

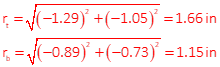
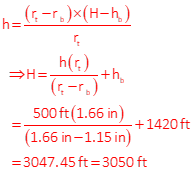
Problem (3)
Prior to photography, a bench mark, point L, was targeted so it would appear on the image. Its elevation is 322.48 m.
The benchmark target appears in the lower right quarter of the photo.
Flying height was 1200 meters above datum, airbase 1500 m
Distances from the side fiducials to the target image were measured multiple times using a magnifying glass scale. The average values are:
| From | Dist, mm |
| A | 177.49 |
| C | 95.16 |
Camera calibration data:
f = 152.0539 mm
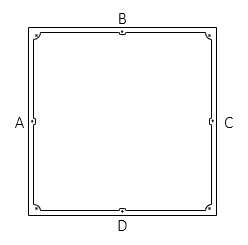
Side fiducial coordinates
 |
|||
| Mark | x, mm | y, mm | |
| A | -111.9902 | 0.0050 | |
| B | 0.0520 | 112.0824 | |
| C | 112.1084 | -0.0052 | |
| D | 0.0025 | -111.0002 | |
What are the ground coordinates of the benchmark? Compute to nearest 0.01 m.
Sketches
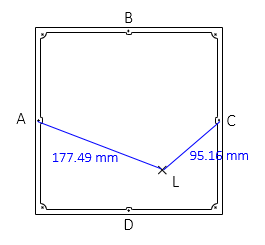
Inverse line A to C

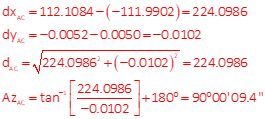
Solve angle at A
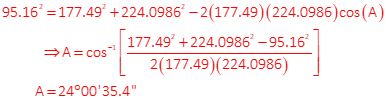
Forward comp A to L:
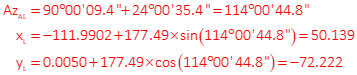
Compute ground coordinates:

Answers:
X = 289.36 m Y = -416.80 m
Problem (4)
Two Section corners are targeted before aerial photography is flown. The flight will be in the direction of the Section line between the corners and will use a standard 6 inch focal length camera with a 9 inch by 9 inch negative format. The elevation of both corners is approximately 1150 ft and horizontal distance between them is 5272.36 ft. For both corners to appear on a single photo, what is the minimum flying height above datum that can be used? Determine to nearest 10 ft.
The section line must fit along a 9 inch width of the photo.
Sketch:
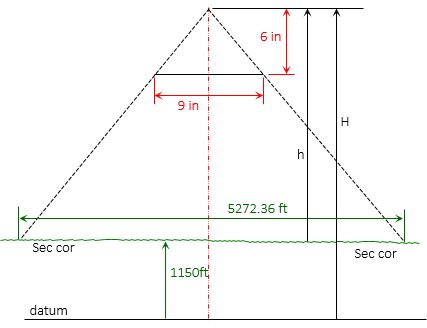
A simple proportion can be set up to solve for the height above the ground, h, to which the Section line's elevation is added.