Solutions: Solving Solutions
Use a Taylor Series approximation to compute the variable values in Problems 3 and 4. Determine to 0.1.
Problem (1)
Determine the values for a, b, and c to 0.1 for the following equations.
2a - 4b + 3c = 14.5
-a + 2b + c = -6.0
5a - b - 4c = 8.0
By substitution
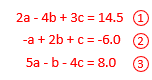


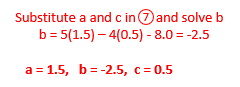
Problem (2)
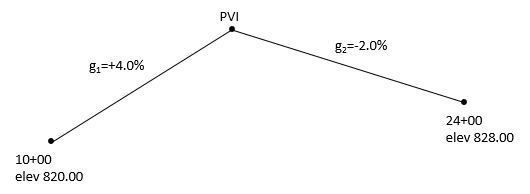
A +4.0% grade is followed by a -2.0% grade on a vertical alignment. Using the information shown below, what are the station and elevation of the PVI?
Using E for elevations and S for stations,
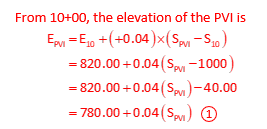
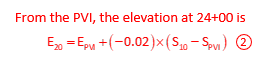
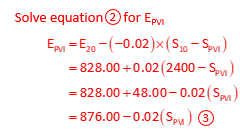
Two equations in two unknowns, Solve using substitution.
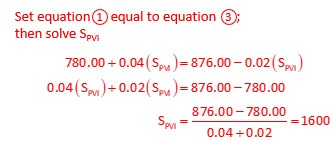
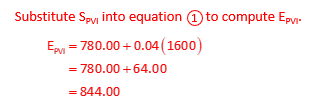
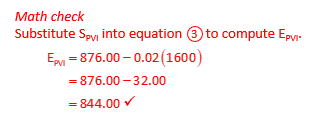
Station is 16+00; Elev = 844.00
Use a Taylor Series approximation to compute the variable values in Problems 3 and 4. Determine to 0.1.
Problem (3)
0.5x3 - 4x2 + 2.5x = -79.2
Start with xo= -2
Partial derivative of the function
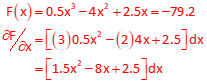
First iteration
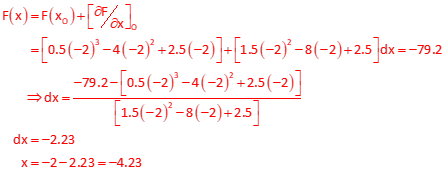
Second iteration
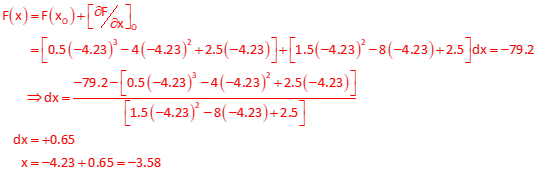
Third iteration
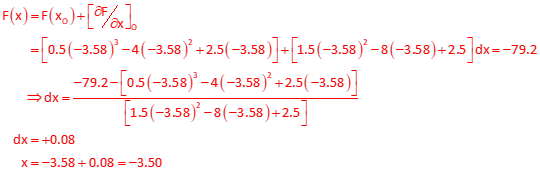
Since the correction is less than 0.1, we can stop.
Math check
0.5(-3.5)3 - 4(-3.5)2 + 2.5(-3.5) = -79.19 check
Answer: x = -3.5
Problem (4)

Start with xo = 5 and yo = -7
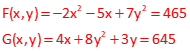
Partial derivatives of each function.
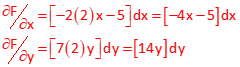
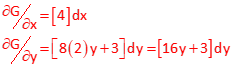
Set up Taylor Series and substitute in initial approximations,
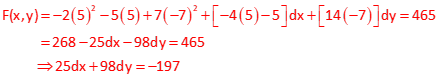
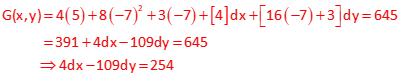
There are two equations in two unknowns. Solve the equations simultaneously.
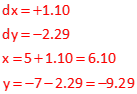
Second iteration:
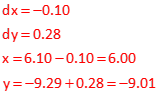
Third iteration.
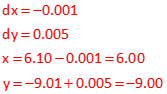
dx and dy small enough in the third iteration so can stop.
Answer: x=6.0, y=-9.0