Solution: COGO Intersections and Transformations

Problem (2)

Additional digits will be carried to minimize rounding errors

The surveyor's Project is the From system, the RPC GIS is the To system. Points E21 and SE21 are used to determine coordinate transformaton parameters.

(1) Coordinates of SE21 in the Project system

(2) Scale, S

Scale is the proportion between line E21-SE21's length in the Project and GIS systems. Need the line's length in the GIS system.

Because Project is in feet and GIS is in meters, be sure to carry the dimensions.

Note that scale is approximately the metric conversion (0.3048 meters per survey foot). It's not exact because it also takes into account random measurement errors and ground-to-grid conversion.

(2) Rotation angle, ρ

The rotation angle is between the Project and GIS azimuths of line E21-SE21. Project azimuth is South: Az_Project = 180°00'00"; must compute the GIS azimuth.

(4) Translations, T_N and T_E

Use point E21. Remember to carry units and make sure they cancel correctly.

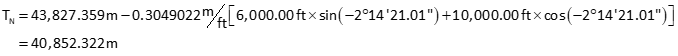
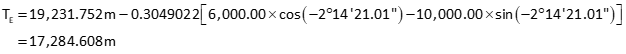
(5) Set up the transformation equations

Include units.

(6) You really should check the transformation equations using the other known point, SE21.

I'll leave that up to you.

(7) Use the projection equations to determine the GIS coordinates of the three parcel corners.

Transformed corner coordinates are (comps left to user):

(8) Inverse calculation clockwise around the traverse.

Results shown (comps left to user):