Solution: COGO Fitting Curves

Problem (1)

Part (a)

What is the diameter of the curve tangent to all three sides of the triangle? 

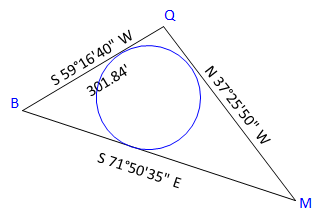
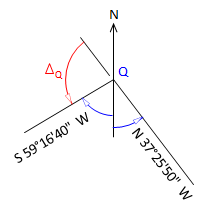
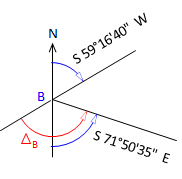
This is a Three-tangent Arc condition. The difference for the discussion in Chapter I is that the three lines close to form a triangle. To solve the circle radius requires the two Δ (deflection) angle between the successive lines. Since the lines close to form a triangle, there are three different Δ angle combinations: Q & B, B & M, M & Q. Each combination will result in the same radius.

Compute the deflection angles at points Q and B.

Solve the radius.

Radius = 97.69'

For a math check, try another Δ angle combination.

Part (b)

What is the diameter of the circle passing through the triangles' verticies?

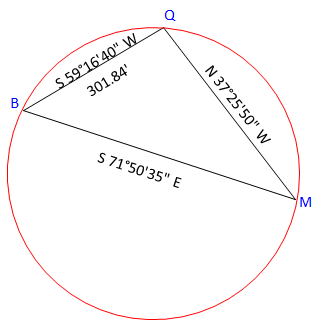
Solution

Since we need coordinates, we'll start with 100.00'N, 500.00'E at point Q.

Compute coordinates at point B.

To get the coordinates of point M requires a direction-direction intersection. For that, we need to compute enough of the triangle to to perform a Forward Computation from point B.

Angles first...

Then side BM by Law of Sines

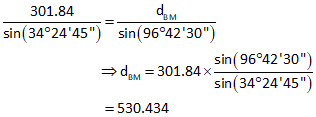
Now the coordinates of point M

So much for the easy part. Now we have to compute the four parameters (A-D) to compute the radius point coordinates

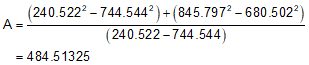
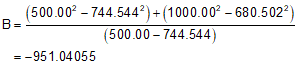
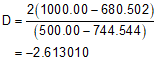
The radius point coordinates are

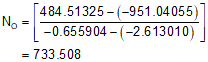
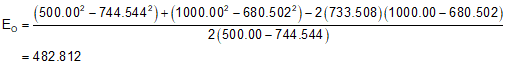
And finally, the radius is

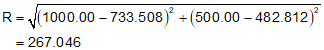
Radius = 267.05'